题目内容
17.已知sin(α+$\frac{π}{3}$)=-$\frac{1}{2}$,α∈(0,π),则cosα=( )| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
分析 利用构造思想,cosα=cos($α+\frac{π}{3}-\frac{π}{3}$)根据和与差的公式打开求解即可.=cos($α+\frac{π}{3}$)cos$\frac{π}{3}$
解答 解:sin(α+$\frac{π}{3}$)=-$\frac{1}{2}$<0
α∈(0,π),
$α+\frac{π}{3}$∈($\frac{π}{3}$,$\frac{4π}{3}$),
∴$α+\frac{π}{3}$∈(π,$\frac{4π}{3}$)
cos($α+\frac{π}{3}$)=$-\frac{\sqrt{3}}{2}$.
那么:cosα=cos($α+\frac{π}{3}-\frac{π}{3}$)=cos($α+\frac{π}{3}$)cos$\frac{π}{3}$+sin(α+$\frac{π}{3}$)sin$\frac{π}{3}$=$-\frac{\sqrt{3}}{2}$.
故选:D.
点评 本题主要考察了同角三角函数关系式和和与差公式的应用,构造思想,属于基本知识的考查.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
7.设集合An={1,2,3,…,n}(n∈N*,n≥3),记An中的元素组成的非空子集为$A_i^'$(i∈N*,i=1,2,3,…,2n-1),对于?i∈{1,2,3,…,2n-1},$A_i^'$中的最小元素和为Sn,则S5=( )
| A. | 32 | B. | 57 | C. | 75 | D. | 480 |
9.已知数列{an}中,a3=2,a6=1,若{ $\frac{1}{1+{a}_{n}}$ }是等差数列,则a11等于( )
| A. | 0 | B. | $\frac{1}{6}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
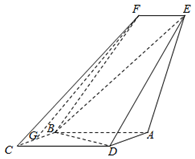 如图,四边形ABCD是平行四边形,平面AED⊥平面ABCD,EF∥AB,AB=2,BC=EF=1,AE=$\sqrt{6}$,DE=3,∠BAD=60°,G为BC的中点.
如图,四边形ABCD是平行四边形,平面AED⊥平面ABCD,EF∥AB,AB=2,BC=EF=1,AE=$\sqrt{6}$,DE=3,∠BAD=60°,G为BC的中点.