题目内容
7.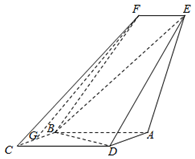 如图,四边形ABCD是平行四边形,平面AED⊥平面ABCD,EF∥AB,AB=2,BC=EF=1,AE=$\sqrt{6}$,DE=3,∠BAD=60°,G为BC的中点.
如图,四边形ABCD是平行四边形,平面AED⊥平面ABCD,EF∥AB,AB=2,BC=EF=1,AE=$\sqrt{6}$,DE=3,∠BAD=60°,G为BC的中点.(1)求证:FG∥平面BED
(2)求三棱锥B-DAE的体积.
分析 (1)连接AC交BD于O,连接OE,可得EFGO为平行四边形⇒GF∥OE,又GF?面BED,OE?面DEB⇒FG∥平面BED;
(2)延长DA,作EH⊥DA垂足为H,由平面AED⊥平面ABCD,⇒EH⊥平面ABCD,⇒EH=DEsin∠DEA=$\sqrt{5}$,即三棱锥B-DAE的体积V=$\frac{1}{3}×\frac{1}{2}AB×AD×sin6{0}^{0}×EH=\frac{\sqrt{15}}{6}$
解答 解:(1)连接AC交BD于O,连接OE,OG⇒OG∥$\frac{1}{2}$CD∥EF,OG=$\frac{1}{2}CD$=EF,
EFGO为平行四边形⇒GF∥OE,又GF?面BED,OE?面DEB⇒FG∥平面BED;
(2)延长DA,作EH⊥DA垂足为H,
由平面AED⊥平面ABCD,
∵DA=平面AED∩平面ABCD,EH?平面AED⇒EH⊥平面ABCD,
cos∠EDA=$\frac{D{E}^{2}+D{A}^{2}-A{E}^{2}}{2DE•DA}=-\frac{2}{3}$⇒sin∠EDA=$\frac{\sqrt{5}}{3}$
⇒EH=DEsin∠DEA=$\sqrt{5}$
∴三棱锥B-DAE的体积V=$\frac{1}{3}×\frac{1}{2}AB×AD×sin6{0}^{0}×EH=\frac{\sqrt{15}}{6}$..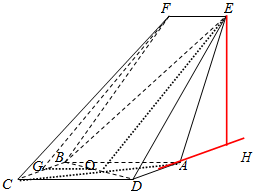
点评 本题考查了线面平行的判定,几何体的体积,属于中档题.

练习册系列答案
相关题目
17.已知sin(α+$\frac{π}{3}$)=-$\frac{1}{2}$,α∈(0,π),则cosα=( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
18.已知平面向量$\overrightarrow a=(1,2)$,$\overrightarrow b=(-2,m)$,且$\overrightarrow a∥\overrightarrow b$,则m等于( )
| A. | 4 | B. | 3 | C. | -4 | D. | -3 |
19.函数$f(x)=Asin(ωx+φ),(ω>0,-\frac{π}{2}<φ<\frac{π}{2})$的部分图象如图所示,则A,ω,φ的值分别是( )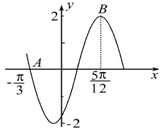

| A. | 1,$2,-\frac{π}{6}$ | B. | 2,$2,-\frac{π}{3}$ | C. | 1,$4,-\frac{π}{6}$ | D. | 2,$4,\frac{π}{3}$ |