题目内容
6.在钝角△ABC中a<b<c,且a=2,b=3,则c的取值范围是$(\sqrt{13},5)$.分析 由在钝角△ABC中a<b<c,可得C为钝角.因此cosC=$\frac{{2}^{2}+{3}^{2}-{c}^{2}}{2×2×3}$<0,2+3>c,即可得出.
解答 解:由在钝角△ABC中a<b<c,∴C为钝角.
∴cosC=$\frac{{2}^{2}+{3}^{2}-{c}^{2}}{2×2×3}$<0,2+3>c,
解得$\sqrt{13}<c<$5.
故答案为:$(\sqrt{13},5)$.
点评 本题考查了余弦定理、三角形三边大小关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
17.已知sin(α+$\frac{π}{3}$)=-$\frac{1}{2}$,α∈(0,π),则cosα=( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
14.在△ABC中,角A、B、C所对的边分别是a、b、c,若$a=\sqrt{6}$,b=2,A=60°,则B=( )
| A. | 30° | B. | 45° | C. | 135° | D. | 45°或135° |
11.设f(x)为定义在R上的奇函数,当x≥0时,f(x)=3x+1-3,则f(-1)的值为( )
| A. | -6 | B. | -3 | C. | -2 | D. | 6 |
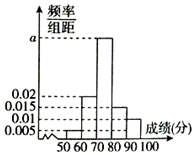 为了了解某学校高二年级学生的物理成绩,从中抽取n名学生的物理成绩(百分制)作为样本,按成绩分成5组:[50,60),[60,70),[70,80),[80,90),[90,100],频率分布直方图如图所示,成绩落在[70,80)中的人数为20.
为了了解某学校高二年级学生的物理成绩,从中抽取n名学生的物理成绩(百分制)作为样本,按成绩分成5组:[50,60),[60,70),[70,80),[80,90),[90,100],频率分布直方图如图所示,成绩落在[70,80)中的人数为20.