题目内容
函数f（x）=x2+x+b，函数g（x）=ex-f′（x）的零点所在的区间是[k，k+1]（k∈Z），则k的值等于（ ）
| A、-1 | B、0 | C、1 | D、0或1 |
考点：二分法求方程的近似解
专题：函数的性质及应用
分析：对函数f（x）求导后，可得函数g（x）=ex-f′（x）的解析式，进而根据g（0）=0可得满足条件的k值．
解答：
解：∵函数f（x）=x2+x+b，
∴f′（x）=2x+1，
∴g（x）=ex-f′（x）=ex-（2x+1），
∵g（0）=0，
故函数g（x）=ex-f′（x）的零点所在的区间是[0，1]，
故k=0，
故选：B
∴f′（x）=2x+1，
∴g（x）=ex-f′（x）=ex-（2x+1），
∵g（0）=0，
故函数g（x）=ex-f′（x）的零点所在的区间是[0，1]，
故k=0，
故选：B
点评：本题考查的知识点是导函数，函数的零点，其中熟练掌握函数零点的存在定理是解答的关键．
练习册系列答案
相关题目
下列函数中，既是偶函数又在（0，+∞）单调递增的函数是（ ）
A、y=-
| ||
| B、y=lgx | ||
| C、y=cosx | ||
| D、y=e|x| |
把函数y=cos（x-
）向左平移m（m＞0）个单位，所得的图象关于y轴对称，则m的最小值为（ ）
| π |
| 6 |
A、
| ||
B、
| ||
C、
| ||
D、
|
函数y=
+
的定义域为（ ）
| ||
| x |
| x-2x2 |
A、（
| ||
B、（0，
| ||
C、[0，
| ||
D、[
|
定义在R上的函数f（x）不是常数函数，且满足对任意的x有f（x-1）=f（x+1），f（2-x）=f（x），下列5个结论：
①f（x）是单调函数，
②f（x）的图象关于x=1对称，
③f（x）是周期函数，
④f（x）是偶函数，
⑤f（x）有最大值和最小值．
其中真命题是（ ）
①f（x）是单调函数，
②f（x）的图象关于x=1对称，
③f（x）是周期函数，
④f（x）是偶函数，
⑤f（x）有最大值和最小值．
其中真命题是（ ）
| A、②③④ | B、②③⑤ |
| C、①②⑤ | D、①②③ |
下面给出的四个点中，位于
，表示的平面区域内的点是（ ）
|
| A、（-4，1） |
| B、（2，2） |
| C、（0，4） |
| D、（-2，1） |
等差数列{an}中，已知a5+a7=10，Sn是{an}的前n项和，S11等于（ ）
| A、45 | B、50 | C、55 | D、60 |
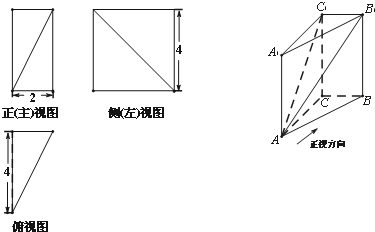某几何体ABC-A1B1C1的三视图和直观图如图所示．