题目内容
1.在60°角内有一点P,到两边的距离分别为1cm和2cm,则P到角顶点的距离为$\frac{2\sqrt{21}}{3}$.分析 根据题意做出图形,再根据直角三角形的知识和勾股定理即可求出.
解答  解:过点P分别做PA⊥OM,PB⊥ON,延长BP延长线与AM交于点C,
解:过点P分别做PA⊥OM,PB⊥ON,延长BP延长线与AM交于点C,
由∠MON=60°,
∴∠ACB=30°,
又AP=1,
∴CP=2AP=2,又BP=2,
∴BC=BP+CP=2+2=4,
在直角三角形ABF中,
tan∠OCB=tan30°=$\frac{OB}{BC}$,
∴OB=BCtan30°=4×$\frac{\sqrt{3}}{3}$=$\frac{4\sqrt{3}}{3}$,
在直角三角形OBP中,根据勾股定理得:OP=$\sqrt{O{B}^{2}+B{P}^{2}}$=$\frac{2\sqrt{21}}{3}$.
故答案为$\frac{2\sqrt{21}}{3}$
点评 此题考查了解三角形的运算,涉及的知识有:直角三角形中30°角所对的直角边等于斜边的一半的性质,锐角三角函数以及勾股定理,其中作出辅助线是本题的突破点,熟练掌握直角三角形的性质及锐角三角函数定义是解本题的关键.

练习册系列答案
相关题目
11.“三元一次方程组的系数矩阵恰为单位矩阵”是“该方程组有唯一解”的( )条件.
| A. | 充分非必要 | B. | 必要非充分 | ||
| C. | 充要 | D. | 既非充分也非必要 |
16.下列四类函数中,具有性质“对任意的x>0,y>0,函数f(x)满足[f(x)]y=f(xy)”的是( )
| A. | 指数函数 | B. | 对数函数 | C. | 一次函数 | D. | 余弦函数 |
6.如图,小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的体积为( )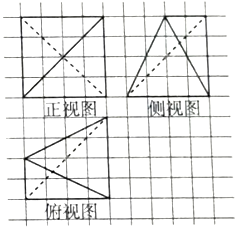

| A. | 8$\sqrt{3}$ | B. | $\frac{80}{3}$ | C. | 16$\sqrt{3}$ | D. | 32 |
13.已知O、A、B是平面上的三个点,直线AB上有一个点C,满足$2\overrightarrow{AC}+\overrightarrow{CB}=\overrightarrow 0$,则$\overrightarrow{OC}$=( )
| A. | $-\frac{1}{3}\overrightarrow{OA}+\frac{2}{3}\overrightarrow{OB}$ | B. | $\frac{2}{3}\overrightarrow{OA}-\frac{1}{3}\overrightarrow{OB}$ | C. | $-\overrightarrow{OA}+2\overrightarrow{OB}$ | D. | $2\overrightarrow{OA}-\overrightarrow{OB}$ |