题目内容
20．在平面内，过定点P的直线mx+y-1=0与过定点Q的直线x-my+3=0相交与点M，则|MP||MQ|的最大值是（ ）| A． | $\frac{{\sqrt{10}}}{2}$ | B． | $\sqrt{10}$ | C． | 10 | D． | 5 |
分析 由已知得P（0，1），Q（-3，0），过定点P的直线mx+y-1=0与过定点Q的直线x-my+3=0垂直，M位于以PQ为直径的圆上，由此能求出|MP||MQ|的最大值．
解答 解：∵在平面内，过定点P的直线mx+y-1=0与过定点Q的直线x-my+3=0相交与点M，
∴P（0，1），Q（-3，0），
∵过定点P的直线mx+y-1=0与过定点Q的直线x-my+3=0垂直，
∴M位于以PQ为直径的圆上，
∵|PQ|=$\sqrt{9+1}=\sqrt{10}$，
∴|MP|2+|MQ|2=10≥2•|MP||MQ|，
∴|MP||MQ|≤5．
∴|MP||MQ|的最大值为5．
故选：D．
点评 本题考查两线段乘积的最大值的求法，是中档题，解题时要认真审题，注意两点间距离公式的合理运用．
练习册系列答案
阅读快车系列答案
相关题目
10．已知f（x）=$\frac{{{x^2}-1}}{x+1}$，则f（f（-2））=（ ）
| A． | 2 | B． | 0 | C． | -2 | D． | -4 |
11．如果$0＜{log_{\frac{1}{2}}}x$$＜{log_{\frac{1}{2}}}y$，那么（ ）
| A． | 0＜y＜x＜1 | B． | 0＜x＜y＜1 | C． | y＞x＞1 | D． | x＞y＞1 |
8．定义：底面是正三角形，侧棱与底面垂直的三棱柱叫做正三棱柱，将正三棱柱截去一个角，（如图1所示，M，N分别为AB，BC的中点）得到几何体如图2．则该几何体按图2所示方向的侧视图为（ ）
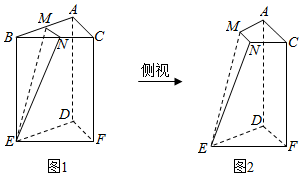
| A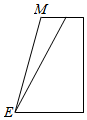． |  | B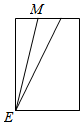． |  | C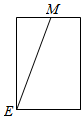． |  | D． |  |
5．某商场五一记性抽奖促销活动，当人在该商场消费的顾客即可参加抽奖活动抽奖情况如下：
抽奖中有9个大小形状完全相同的小球，其中4个红球、3个白球、2个黑球（每次只能抽取一个，且不放回抽取），第一种抽奖方式：若抽得红球，获奖金10元；若抽得白球，获奖金20元；若抽得黑球，获奖金40元，第二种抽奖方式：抽到白球或黑球才中奖，若抽到白球，获奖金50元；若抽到黑球获奖金100元．
（1）若某顾客在该商场当日消费金额为2000元，用第一种抽奖方式进行抽奖，求获得奖金70元的概率；
（2）若偶顾客在该商场当日消费金额为1200元，请同学们告诉这位顾客哪种抽奖方式对他有利．
| 消费金额X（元） | [500，1000） | [1000，1500） | [1500，+∞） |
| 抽奖次数 | 1 | 2 | 4 |
（1）若某顾客在该商场当日消费金额为2000元，用第一种抽奖方式进行抽奖，求获得奖金70元的概率；
（2）若偶顾客在该商场当日消费金额为1200元，请同学们告诉这位顾客哪种抽奖方式对他有利．
12．下列各组函数相等的是（ ）
| A． | $f（x）=\frac{{{x^2}-1}}{x-1}与g（x）=x+1$ | B． | $f（x）=1与g（x）=\frac{{\sqrt{x^2}}}{x}$ | ||
| C． | f（x）=（x-2）0与g（x）=1 | D． | $f（x）=\sqrt{x^4}与g（x）={x^2}$ |
已知正方形ABCD，PA⊥平面ABCD，且$PA=AB=\sqrt{2}$，E是AB中点．
如图所示，正三棱锥P-ABC的底面边长为a，高PO为h，求它的侧棱PA和斜高PD的长．