题目内容
9. 已知正方形ABCD,PA⊥平面ABCD,且$PA=AB=\sqrt{2}$,E是AB中点.
已知正方形ABCD,PA⊥平面ABCD,且$PA=AB=\sqrt{2}$,E是AB中点.(1)求证:AE⊥平面PBC;
(2)求点E到平面PAC的距离.
分析 (1)证明BC⊥AE.PB⊥AE,即可证明AE⊥平面PBC.
(2)利用点E到平面PAC的距离为点B到平面PAC的距离的$\frac{1}{2}$.连接BD,交AC于点O,则AC⊥BO,求解BO即可.
解答 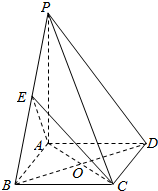 解:(1)证明:∵PA⊥平面ABCD,BC?平面ABCD∴PA⊥BC.
解:(1)证明:∵PA⊥平面ABCD,BC?平面ABCD∴PA⊥BC.
又∵正方形ABCD,∴AB⊥BC.∵PA∩AB=A,∴BC⊥平面PAB∵AE?平面PAB,∴BC⊥AE.
又∵PA=AB,E是AB中点,∴PB⊥AE.∵PB∩BC=B,∴AE⊥平面PBC.
(2)∵E是AB中点,
∴点E到平面PAC的距离为点B到平面PAC的距离的$\frac{1}{2}$.
连接BD,交AC于点O,则AC⊥BO,
又∵PA⊥平面ABCD,BO?平面ABCD,∴PA⊥BO.
∵AC∩PA=A,∴BO⊥平面PAC.
∴BO为点B到平面PAC的距离.
∵$AB=\sqrt{2}$,∴BO=1.
∴$点E到平面PAC的距离为\frac{1}{2}BO=\frac{1}{2}$.
点评 本题考查空间点线面距离的求法,直线与平面垂直的判定定理的应用,考查空间想象能力以及距离投篮能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.椭圆4x2+y2=1的长轴等于( )
| A. | 1 | B. | 2 | C. | 4 | D. | $\frac{1}{2}$ |
20.在平面内,过定点P的直线mx+y-1=0与过定点Q的直线x-my+3=0相交与点M,则|MP||MQ|的最大值是( )
| A. | $\frac{{\sqrt{10}}}{2}$ | B. | $\sqrt{10}$ | C. | 10 | D. | 5 |
4.已知过抛物线y2=4x的焦点F的直线交该抛物线于A、B两点,|AF|=2,则|BF|=( )
| A. | 1 | B. | 2 | C. | 4 | D. | 4 |
14.已知A(2,3),B(-4,0),P(-3,1),Q(-1,2),试判断直线AB与PQ的位置关系( )
| A. | 平行 | B. | 垂直 | C. | 重合 | D. | 不能确定 |
1.已知△ABC中,bcosB=ccosC,则△ABC的形状为( )
| A. | 直角三角形 | B. | 等腰三角形 | ||
| C. | 等腰或直角三角形 | D. | 等边三角形 |