题目内容
11.已知函数f(x)=log2(2x+1).(1)若函数g(x)的图象与f(x)的图象关于y轴对称,求y=f(x)+g(x)的值域;
(2)记f-1(x)为函数,f(x)的反函数,若关于x的方程f-1(x)=m+f(x)在[1,2]上有解,求m的取值范围.
分析 (1)求出g(x),再求y=f(x)+g(x)的值域;
(2)先求得反函数f-1(x)=log2(2x-1)(x>0),构造函数,利用复合函数的单调性求得函数的值域.
解答 解:(1)∵函数g(x)的图象与f(x)的图象关于y轴对称,
∴g(x)=log2(2-x+1).
y=f(x)+g(x)=log2(2x+1)+log2(2-x+1)=log2(2+2-x+2x)≥2,
∴y=f(x)+g(x)的值域为[2,+∞);
(2)∵f(x)=log2(2x+1),
∴f-1(x)=log2(2x-1)(x>0),
∴m=f-1(x)-f(x)=log2(2x-1)-log2(2x+1)=log2$\frac{{2}^{x}-1}{{2}^{x}+1}$=log2(1-$\frac{2}{{2}^{x}+1}$)
当1≤x≤2时,$\frac{2}{5}$≤$\frac{2}{{2}^{x}+1}$≤$\frac{2}{3}$,
∴$\frac{1}{3}$≤1-$\frac{2}{{2}^{x}+1}$≤$\frac{3}{5}$,
∴m的取值范围是[log2$\frac{1}{3}$,log2$\frac{3}{5}$].
点评 本题主要考查函数与方程的综合运用,主要涉及了函数的值域以及构造函数研究函数的性质等问题,还考查了转化思想和构造转化函数的能力.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
1.如图是某算法的程序框图,若输出y值为4,则输入的x最大负整数是( )


| A. | -3 | B. | -2 | C. | -1 | D. | -4 |
2.已知复数z1,z2,则下列说法中正确的是( )
| A. | |z1|+|z2|>|z1+z2| | B. | |z1|-|z2|>|z1-z2| | C. | |z1|+|z2|≥|z1+z2| | D. | |z1|-|z2|≥|z1-z2| |
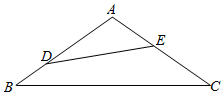 某小区要将如图所示的一块三角形边角地修建成花圃.根据建造规划,要求横穿花圃的直线灌溉水道DE恰好把花圃分成面积相等的两部分(其中D在边AB上,E在边AC上)已知AB=AC=2a,∠BAC=120°
某小区要将如图所示的一块三角形边角地修建成花圃.根据建造规划,要求横穿花圃的直线灌溉水道DE恰好把花圃分成面积相等的两部分(其中D在边AB上,E在边AC上)已知AB=AC=2a,∠BAC=120°