题目内容
16.已知数列{an}满足an+1=2+an(n∈N*),且a1=1.(1)求数列{an}的通项公式及{an}的前n项和Sn;
(2)设bn=${2}^{{a}_{n}}$,求数列{bn}的前n项和Tn;
(3)证明:$\frac{{T}_{n}{T}_{n+2}}{{T}_{n+1}^{2}}$<1(n∈N*)
分析 (1)先由an+1=2+an(n∈N*),a1=1得到,数列{an}是以1为首项,以2为公差的等差数列,根据等差数列的通项公式和前n项和公式,写出an和Sn,
(2)写出bn的通项公式,数列{bn}是以2为首项,以4为公比的等比数列,写出前n项和公式,
(3)分别写出Tn•Tn+2和${T}_{n+1}^{2}$,化简比较两者的大小,即可证明.
解答 解:(1)∵数列{an}满足an+1=2+an(n∈N*),且a1=1.
∴an+1-an=2,
∴数列{an}是以1为首项,以2为公差的等差数列,
∴an=1+2(n-1)=2n-1,
即an=2n-1,(n∈N*),
∴{an}的前n项和Sn=$\frac{n(1+2n-1)}{2}$=n2,
(2)∵bn=${2}^{{a}_{n}}$=22n-1=$\frac{1}{2}$•4n=2•4n-1,
∴数列{bn}是以2为首项,以4为公比的等比数列,
又数列{bn}前n项和为Tn,则Tn=$\frac{2}{3}({4}^{n}-1)$,
(3)$\frac{{T}_{n}{T}_{n+2}}{{T}_{n+1}^{2}}$$\frac{{4}^{2n+2}-{4}^{n}-{4}^{n+2}+1}{{4}^{2n+2}-2•{4}^{n+1}+1}$(n∈N*),
4n+4n+2=$\frac{1}{4}•{4}^{n+1}+4•{4}^{n+1}$=$\frac{17}{4}$•4n+1>2•4n+1,
42n+2-4n-4n+2+1<42n+2-2•4n+1+1,
∴$\frac{{T}_{n}{T}_{n+2}}{{T}_{n+1}^{2}}$<1(n∈N*).
点评 本题考查等比等差数列的通项公式及前n项和公式,考查综合观察和转化能力,属于中档题.

 活力课时同步练习册系列答案
活力课时同步练习册系列答案| 公务员 | 教师 | 合计 | |
| 同意延迟退休 | 40 | n | 70 |
| 不同意延迟退休 | m | 20 | p |
| 合计 | 50 | 50 | 100 |
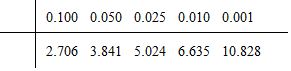
(Ⅰ)求上表中m,n,p的值,并问是否有95%的把握认为“是否同意延迟退休与不同的职业有关”.
(Ⅱ)现用分层抽样方法(按同意和不同意分二层)从调查的两个职业人群中各抽取五人,然后从每个职业的五人中各抽取两人,将这四人中的同意延迟退休的人数记为x,求x的分布列和期望.