题目内容
17.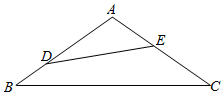 某小区要将如图所示的一块三角形边角地修建成花圃.根据建造规划,要求横穿花圃的直线灌溉水道DE恰好把花圃分成面积相等的两部分(其中D在边AB上,E在边AC上)已知AB=AC=2a,∠BAC=120°
某小区要将如图所示的一块三角形边角地修建成花圃.根据建造规划,要求横穿花圃的直线灌溉水道DE恰好把花圃分成面积相等的两部分(其中D在边AB上,E在边AC上)已知AB=AC=2a,∠BAC=120°(1)设AD=x,DE=y,试求y关于x的函数y=f(x)(解析式和定义域);
(2)为使得灌溉水道DE的建设费用最少,试确定点D的具体位置.
分析 (1)先根据三角形面积,求得x与AE的关系,进而根据余弦定理把x和AE的关系带入求得x和y的关系.
(2)根据均值不等式求得y的最小值,求得等号成立时的x的值即可.
解答 解:(1)∵AB=AC=2a,∠BAC=120°,
∴△ABC的面积是$\sqrt{3}$a2,
∴△ADE的面积是$\frac{\sqrt{3}}{2}$a2,
∵AD=x,DE=y,
∴①$\frac{\sqrt{3}{a}^{2}}{2}$=$\frac{1}{2}$x×AE×sin60°,
∴AE=$\frac{2{a}^{2}}{x}$,
②y2=x2+AE2-2x•AE•cos60°=x2+AE2-x•AE=x2+($\frac{2{a}^{2}}{x}$)2-2a2,
∴y>0,
∴y=$\sqrt{{x}^{2}+\frac{4{a}^{4}}{{x}^{2}}-2{a}^{2}}$,
又AE=$\frac{2{a}^{2}}{x}$≤2a,∴x≥a,
∵D在AB上,
∴x≤2a,
∴y=$\sqrt{{x}^{2}+\frac{4{a}^{4}}{{x}^{2}}-2{a}^{2}}$ (a≤x≤2a),
(2)y=$\sqrt{{x}^{2}+\frac{4{a}^{4}}{{x}^{2}}-2{a}^{2}}$≥$\sqrt{2•2{a}^{2}-2{a}^{2}}$=$\sqrt{2}$a,
当且仅当x2=$\frac{4{a}^{4}}{{x}^{2}}$,即x=$\sqrt{2}$a时“=”成立,
此时AE=$\sqrt{2}$a,
∴使AD=AE=$\sqrt{2}$a时,DE最短,最短为$\sqrt{2}$a.
点评 本题主要考查基本不等式,以及函数的单调性求最值,考查了学生运用所学知识解决实际问题的能力.

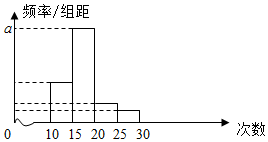 对某校高二学生参加舍去服务次数进行统计.随机抽取M名学生作为样本,得到这M名学生参加舍去服务的次数,根据此数据作出了频数与频率的统计表和频率分布直方图如下:
对某校高二学生参加舍去服务次数进行统计.随机抽取M名学生作为样本,得到这M名学生参加舍去服务的次数,根据此数据作出了频数与频率的统计表和频率分布直方图如下:| 分组 | 频数 | 频率 |
| [10,15) | 10 | 0.25 |
| [15,20) | 25 | n |
| [20,25) | m | p |
| [25,30) | 2 | 0.05 |
| 合计 | M | 1 |
(2)估计高二年级学生参加社区服务次数的平均数和中位数(保留一位小数).
| A. | (0,$\frac{3}{4}$]∪[$\frac{3}{2}$,+∞) | B. | (0,$\frac{3}{4}]$ | C. | [$\frac{3}{2}$,+∞) | D. | [$\frac{3}{4},\frac{3}{2}]$ |