题目内容
1.如图:抛物线y2=x与直线x=ty-1交于A,B两点,点B关于x轴的对称点为C,则直线AC在x轴上的截距( )
| A. | 1 | B. | $\frac{1}{2}$ | ||
| C. | $\frac{1}{4}$ | D. | 不是定值,与t的值相关 |
分析 将直线的方程代入抛物线的方程,消去x得到关于y的一元二次方程,再结合根与系数的关系,确定直线AC的方程,令y=0,从而解决问题.
解答 解:直线x=ty-1代入抛物线方程y2=x得:y2-ty+1=0,
设点A(xA,yA),B(xB,yB)
则yAyB=1,
B点关于x轴的对称点为C(xB,-yB),
直线AC的方程为:y-yB=$\frac{{y}_{A}+{y}_{B}}{{x}_{A}-{x}_{B}}$(x-xB),
令y=0得:x=xB+$\frac{{x}_{A}-{x}_{B}}{{y}_{A}+{y}_{B}}$×(-yB)=xB+1×(-yB2+yAyB)=yAyB=1,
即直线AC在x轴上的截距为1.
故选:A.
点评 本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到直线与抛物线的位置关系,韦达定理等相关知识,解题时要注意合理地进行等价转化.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.已知双曲线:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1,F2,焦距为2c,直线y=$\sqrt{3}$(x+c)与双曲线的一个交点M满足∠MF1F2=2∠MF2F1,则双曲线的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{3}$+1 |
12.“p∨q为真”是“¬p为假”的( )条件.
| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充要 | D. | 既不充分也不必要 |
9.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的左、右焦点分别为F1、F2,其一条渐近线为x+$\sqrt{2}$y=0,点M在双曲线上,且MF1⊥x轴,若F2同时为抛物线y2=12x的焦点,则F1到直线F2M的距离为( )
| A. | $\frac{{3\sqrt{6}}}{5}$ | B. | $\frac{{5\sqrt{6}}}{6}$ | C. | $\frac{5}{6}$ | D. | $\frac{6}{5}$ |
16.阅读如图所示的程序框图,若运行该程序后输出的y的值为4,则输入的实数x的值为( )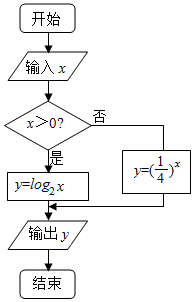

| A. | 4 | B. | 16 | C. | -1或16 | D. | -1或$\frac{1}{16}$ |
13.设F1,F2是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右两个焦点,若双曲线右支上存在一点P,使($\overrightarrow{OP}$+$\overrightarrow{O{F}_{2}}$)•($\overrightarrow{OP}$-$\overrightarrow{O{F}_{2}}$)=0(O为坐标原点),且|PF1|=$\sqrt{2}$|PF2|,则双曲线的离心率为( )
| A. | $\frac{\sqrt{3}+2}{2}$ | B. | $\sqrt{3}$+2 | C. | $\frac{\sqrt{3}+\sqrt{6}}{2}$ | D. | $\sqrt{3}$+$\sqrt{6}$ |
10.曲线y=x2与x=1及坐标轴围成的封闭区域为Ω1,不等式组$\left\{\begin{array}{l}{0≤x≤1}\\{0≤y≤1}\end{array}\right.$表示的平面区域为Ω2,在区域Ω2内随机取一点,则该点是取自于区域Ω1的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{2}{5}$ |