题目内容
9.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的左、右焦点分别为F1、F2,其一条渐近线为x+$\sqrt{2}$y=0,点M在双曲线上,且MF1⊥x轴,若F2同时为抛物线y2=12x的焦点,则F1到直线F2M的距离为( )| A. | $\frac{{3\sqrt{6}}}{5}$ | B. | $\frac{{5\sqrt{6}}}{6}$ | C. | $\frac{5}{6}$ | D. | $\frac{6}{5}$ |
分析 求出双曲线的渐近线的方程,可得a=$\sqrt{2}$b,由抛物线的焦点坐标,可得c=3,即a2+b2=9,解得a,b,可得双曲线的方程,求得M的坐标和直线MF2的方程,运用点到直线的距离公式计算即可得到所求值.
解答 解:双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的渐近线方程为y=±$\frac{b}{a}$x,
由题意可得$\frac{b}{a}$=$\frac{1}{\sqrt{2}}$,
又抛物线y2=12x的焦点为(3,0),
即有c=3,即a2+b2=9,
解得b=$\sqrt{3}$,a=$\sqrt{6}$,
可得双曲线的方程为$\frac{{x}^{2}}{6}$-$\frac{{y}^{2}}{3}$=1,
令x=-3,可得y=±3$\sqrt{\frac{9}{6}-1}$=±$\frac{\sqrt{6}}{2}$,
可设M(-3,$\frac{\sqrt{6}}{2}$),
直线MF2的方程为y=-$\frac{\sqrt{6}}{12}$x+$\frac{\sqrt{6}}{4}$,
可得F1到直线F2M的距离为$\frac{|-\frac{\sqrt{6}}{12}×(-3)+\frac{\sqrt{6}}{4}|}{\sqrt{1+\frac{6}{144}}}$=$\frac{6}{5}$.
故选:D.
点评 本题考查双曲线的方程和性质,考查点到直线的距离的求法,注意运用抛物线的焦点和双曲线的渐近线方程,以及运算能力,属于中档题.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
19.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的左、右焦点分别是F1,F2,正三角形△AF1F2的顶点A在y轴上,边AF1与双曲线左支交于点B,且$\overrightarrow{A{F}_{1}}$=4$\overrightarrow{B{F}_{1}}$,则双曲线C的离心率的值是( )
| A. | $\frac{\sqrt{3}}{2}$+1 | B. | $\frac{\sqrt{13}+1}{3}$ | C. | $\frac{\sqrt{13}}{3}$+1 | D. | $\frac{\sqrt{3}+1}{2}$ |
20.不等式|x+1|•(2x-1)≥0的解集为( )
| A. | {x|x≥$\frac{1}{2}$} | B. | {x|x≤-1或x≥$\frac{1}{2}$} | C. | {x|x=-1或x≥$\frac{1}{2}$} | D. | {x|x≤$\frac{1}{2}$或x≥-1} |
14.在如图所示的流程图中,若输入a,b,c的值分别为2,4,5,则输出的x=( )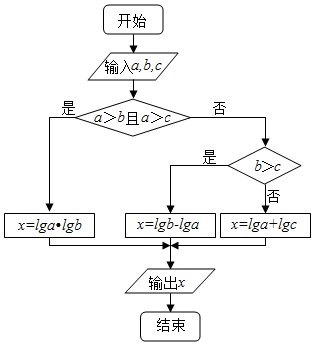

| A. | 1 | B. | 2 | C. | lg2 | D. | 10 |
1.如图:抛物线y2=x与直线x=ty-1交于A,B两点,点B关于x轴的对称点为C,则直线AC在x轴上的截距( )


| A. | 1 | B. | $\frac{1}{2}$ | ||
| C. | $\frac{1}{4}$ | D. | 不是定值,与t的值相关 |

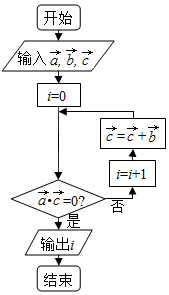 已知$\overrightarrow{a}$=$\overrightarrow{c}$=(-3,3),$\overrightarrow{b}$=(1,0),执行如图所示的程序框图,则输出i的值为( )
已知$\overrightarrow{a}$=$\overrightarrow{c}$=(-3,3),$\overrightarrow{b}$=(1,0),执行如图所示的程序框图,则输出i的值为( )