题目内容
18.若a>0,b>0,且2a+b=1,且$2\sqrt{ab}-4{a^2}-{b^2}$的最大值是$\frac{{\sqrt{2}-1}}{2}$.分析 利用$\sqrt{\frac{4{a}^{2}+{b}^{2}}{2}}≥\frac{2a+b}{2}≥\sqrt{2ab}$,可得$\sqrt{2ab}$≤$\frac{1}{2}$,4a2+b2≥$\frac{1}{2}$,即可得出.
解答 解:∵2a+b=1,a>0,b>0,
∴由$\sqrt{\frac{4{a}^{2}+{b}^{2}}{2}}≥\frac{2a+b}{2}≥\sqrt{2ab}$,可得$\sqrt{2ab}$≤$\frac{1}{2}$,4a2+b2≥$\frac{1}{2}$,
∴S=2$\sqrt{ab}$-(4a2+b2)≤$\frac{\sqrt{2}-1}{2}$,当且仅当b=2a=$\frac{1}{2}$时取等号.
∴S的最大值为$\frac{{\sqrt{2}-1}}{2}$,
故答案为:$\frac{{\sqrt{2}-1}}{2}$.
点评 本题考查了基本不等式及其变形应用,属于基础题.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
9.已知集合A={-2,-1,0,1,2},B={x|-2<x≤2},则A∩B=( )
| A. | {-1,0,1,2} | B. | {-1,0,1} | C. | {-2,-1,0,1} | D. | {-2,-1,0,1,2} |
6.某重点中学为了解高一年级学生身体发育情况,对全校700名高一年级学生按性别进行分层抽样检查,测得身高(单位:cm)频数分布表如表1、表2.
表1:男生身高频数分布表
表2:女生身高频数分布表
(1)求该校高一女生的人数;
(2)估计该校学生身高在[165,180)的概率;
(3)以样本频率为概率,现从高一年级的男生和女生中分别选出1人,设X表示身高在[165,180)学生的人数,求X的分布列及数学期望.
表1:男生身高频数分布表
| 身高(cm) | [160,165) | [165,170) | [170,175) | [175,180) | [180,185) | [185,190) |
| 频数 | 2 | 5 | 14 | 13 | 4 | 2 |
| 身高(cm) | [150,155) | [155,160) | [160,165) | [165,170) | [170,175) | [175,180) |
| 频数 | 1 | 7 | 12 | 6 | 3 | 1 |
(2)估计该校学生身高在[165,180)的概率;
(3)以样本频率为概率,现从高一年级的男生和女生中分别选出1人,设X表示身高在[165,180)学生的人数,求X的分布列及数学期望.
10.从{2,3,4,5,6}中随机选取一个数为a,从{1,2,3,5}中随机选取一个数为b,则b>a的概率是( )
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{5}$ |
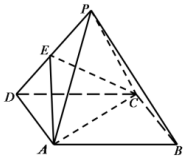 如图,四棱锥P-ABCD中,底面ABCD是平行四边形,且平面PAC⊥平面ABCD,E为PD的中点,PA=PC,AB=2BC=2,∠ABC=60°.
如图,四棱锥P-ABCD中,底面ABCD是平行四边形,且平面PAC⊥平面ABCD,E为PD的中点,PA=PC,AB=2BC=2,∠ABC=60°.