题目内容
是否存在同时满足下列两条件的直线l:(1)l与抛物线y2=8x有两个不同的交点A和B;(2)线段AB被直线l1:x+5y-5=0垂直平分.若不存在,说明理由,若存在,求出直线l的方程.
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:假设存在,设出点的坐标,联立方程可表示出AB的斜率,根据已知条件确定直线AB的斜率,进而求得y1+y2的值,则AB的中点的纵坐标可求,带入直线求得x,进而求得直线AB的方程.
解答:
解:假定在抛物线y2=8x上存在这样的两点A(x1,y1),B(x2,y2).
则有:
⇒(y1+y2)(y1-y2)=8(x1-x2)⇒kAB=
=
∵线段AB被直线l1:x+5y-5=0垂直平分,且kl1=-
,
∴kAB=5,即
=5⇒y1+y2=
.
设线段AB的中点为M(x0,y0),则y0=
=
.
代入x+5y-5=0得x=1.
∴AB中点为M(1,
).故存在符合题设条件的直线,其方程为:y-
=5(x-1),即:25x-5y-21=0.
则有:
|
| (y1-y2) |
| (x1-x2) |
| 8 |
| (y1+y2) |
∵线段AB被直线l1:x+5y-5=0垂直平分,且kl1=-
| 1 |
| 5 |
∴kAB=5,即
| 8 |
| (y1+y2) |
| 8 |
| 5 |
设线段AB的中点为M(x0,y0),则y0=
| y1+y2 |
| 2 |
| 4 |
| 5 |
代入x+5y-5=0得x=1.
∴AB中点为M(1,
| 4 |
| 5 |
| 4 |
| 5 |
点评:本题主要考查了直线与抛物线的关系综合问题.解题过程巧妙运用了错差法把抛物线与直线的斜率问题联系,找到了解决问题的突破口.

练习册系列答案
相关题目
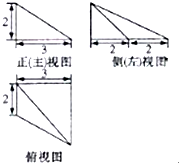
某几何体的三视图(单位:cm)如图所示,则该几何体的体积为:( )

| A、2cm2 | ||
B、
| ||
C、
| ||
| D、6cm2 |
椭圆的焦点坐标为(4,0),(-4,0),椭圆上一点到两焦点的距离之和为10,则椭圆的标准方程为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知圆M:(x+2)2+y2=4,过点P(-1,0)作圆M的互相垂直的两条弦AB,CD,则这两条弦长之和的最大值为( )
A、2
| ||
| B、8 | ||
C、4+2
| ||
D、4
|
 如图,已知矩形ABCD,P为平面ABCD外一点,M、N分别为BC、PD的中点,且满足
如图,已知矩形ABCD,P为平面ABCD外一点,M、N分别为BC、PD的中点,且满足