��Ŀ����
20��ij�̳Ǿ����н���������˿���һ��������Ʒ�ɳ齱���齱�������£�1���齱�������������֣�����a����װ��2������3��������ɫ��ͬ���ļ״����������2���������Ǻ������ý���30Ԫ������û�н��𣬶ҽ�����������Żؼ״��У�����b����װ��3������2��������ɫ��ͬ�����Ҵ����������2���������Ǻ������ý���15Ԫ������û�н��𣬶ҽ�����������Ż��Ҵ��У�
2���齱�����ǣ��˿�����Ʒ�Ľ����100Ԫ���ɸ��ݷ���a�齱һ�Σ���150Ԫ���ɸ��ݷ���b�齱һ�Σ�����ij�˿�����Ʒ�Ľ��Ϊ260Ԫ����ù˿Ϳ��Ը��ݷ���a�齱���λ�b�齱һ�λ�a��b���齱һ�Σ�����֪�˿�A�ڸ��̳�������Ʒ�Ľ��Ϊ350Ԫ��
��1�����˿�Aֻѡ��a���г齱���������������ֵ��
��2��Ҫʹ���������ֵ��˿�AӦ��γ齱��
���� ��1���˿�Aֻѡ��a���г齱������齱��ʽΪ������a�齱���Σ��������ֲ�B��3��$\frac{1}{10}$�����ɴ�������˿�Aֻѡ��a���г齱�������������ֵ��
��2��������bһ�γ��еĸ���P��B��=$\frac{{C}_{3}^{2}}{{C}_{5}^{2}}$=$\frac{3}{10}$������٣��˿�A������a�齱���Σ�������b�齱һ�Σ���ʱ����a�ij鷨�������ֲ�B1����2��$\frac{1}{10}$��������b�ij鷨�������ֲ�B2����1��$\frac{3}{10}$���������ý���Ϊw2�����${E}_{{w}_{2}}$������ڣ��˿�A������b�齱���Σ���ʱ�������ֲ�B����2��$\frac{3}{10}$���������ý���Ϊw3�����${E}_{{w}_{3}}$���ɴ������Ҫʹ���������ֵ��˿�AӦ������a�齱���Σ�������b�齱һ�Σ�
��� �⣺��1���˿�Aֻѡ��a���г齱������齱��ʽΪ������a�齱���Σ�
������aһ�γ��еĸ���P��A��=$\frac{{C}_{2}^{2}}{{C}_{5}^{2}}$=$\frac{1}{10}$��
��ʱ�������ֲ�B��3��$\frac{1}{10}$����
�����ý���Ϊw1����${E}_{{w}_{1}}$=$3��\frac{1}{10}��30=9$��
��˿�Aֻѡ��a���г齱�������������ֵΪ9Ԫ��
��2��������bһ�γ��еĸ���P��B��=$\frac{{C}_{3}^{2}}{{C}_{5}^{2}}$=$\frac{3}{10}$��
����٣��˿�A������a�齱���Σ�������b�齱һ�Σ�
��ʱ����a�ij鷨�������ֲ�B1����2��$\frac{1}{10}$����
����b�ij鷨�������ֲ�B2����1��$\frac{3}{10}$����
�����ý���Ϊw2����${E}_{{w}_{2}}$=$2��\frac{1}{10}��30+1��\frac{3}{10}��15$=10.5��
����ڣ��˿�A������b�齱���Σ���ʱ�������ֲ�B����2��$\frac{3}{10}$����
�����ý���Ϊw3����${E}_{{w}_{3}}$=2��$\frac{3}{10}��15$=9��
��${E}_{{w}_{1}}={E}_{{w}_{3}}��{E}_{{w}_{2}}$��
��Ҫʹ���������ֵ��˿�AӦ������a�齱���Σ�������b�齱һ�Σ�
���� ���⿼����ʵ���������ɢ����������ķֲ��С���ѧ��������Ӧ�ã�����������֤����������������������黯����ת��˼�롢���ν��˼�룬���е��⣮

 ������ϵ�д�
������ϵ�д�| A�� | {x|-1��x��2} | B�� | {x|2��x��3} | C�� | {x|x��3} | D�� | {x|-1��x��2} |
| A�� | k=��2 | B�� | k=$\frac{8}{{e}^{2}}$ | C�� | k=2 | D�� | k=$\frac{4}{{e}^{2}}$+$\frac{{e}^{2}}{4}$ |
| A�� | $1\frac{61}{66}$�� | B�� | 2�� | C�� | $2\frac{3}{22}$�� | D�� | 3�� |
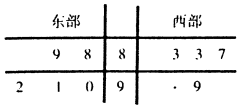 ijʡ����̨Ϊ�˽��ʡ����һ���������Ŀ�������������鶫��������5�����У��õ��ۿ��ý�Ŀ����������λ��ǧ�ˣ����¾�Ҷͼ��ʾ��
ijʡ����̨Ϊ�˽��ʡ����һ���������Ŀ�������������鶫��������5�����У��õ��ۿ��ý�Ŀ����������λ��ǧ�ˣ����¾�Ҷͼ��ʾ������һ�����ֱ�����
��1���������йۿ��ý�Ŀ����ƽ�������������������йۿ��ý�Ŀ����ƽ�������ĸ��ʣ�
��2�����Ž�Ŀ�IJ����������˹��ڶԳ���֪ʶ��ѧϰ���۵����飬���л����dz���ִӹۿ��ý�Ŀ�Ĺ��������ͳ����4λ���ڵ��ܾ�ѧϰ����֪ʶ��ʱ��y����λ��Сʱ��������x����λ���꣩���������˶��ձ��������ʾ��
| ����x���꣩ | 20 | 30 | 40 | 50 |
| �ܾ�ѧϰ����֪ʶʱ��y��Сʱ�� | 2.5 | 3 | 4 | 4.5 |
�ο���ʽ��$\stackrel{��}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{x}^{2}}$��$\stackrel{��}{a}$=$\overline{y}$-$\stackrel{��}{b}$x��
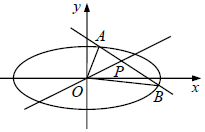 ��֪��P��t��$\frac{1}{2}$������ԲC��$\frac{{x}^{2}}{2}$+y2=1�ڣ���P��ֱ��l����ԲC�ཻ��A��B���㣬�ҵ�P���߶�AB���е㣬OΪ����ԭ�㣮
��֪��P��t��$\frac{1}{2}$������ԲC��$\frac{{x}^{2}}{2}$+y2=1�ڣ���P��ֱ��l����ԲC�ཻ��A��B���㣬�ҵ�P���߶�AB���е㣬OΪ����ԭ�㣮