题目内容
2.网络购物已经成为一种时尚,电商们为了提升知名度,加大了在媒体上的广告投入.经统计,近五年某电商在媒体上的广告投入费用x(亿元)与当年度该电商的销售收入y(亿元)的数据如下表:):| 年份 | 2012年 | 2013年 | 2014 | 2015 | 2016 |
| 广告投入x | 0.8 | 0.9 | 1 | 1.1 | 1.2 |
| 销售收入y | 16 | 23 | 25 | 26 | 30 |
(Ⅱ)2017年度该电商准备投入广告费1.5亿元,利用(Ⅰ)中的回归方程,预测该电商2017年的销售收入.
附:回归直线的斜率和截距的最小二乘估计公式分别为:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n•\overline{x}•\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n•{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$•$\overline{x}$,选用数据:$\sum_{i=1}^{5}$xiyi=123.1,$\sum_{i=1}^{5}$x${\;}_{i}^{2}$=5.1.
分析 (Ⅰ)根据表中数据计算$\overline{x}$=1,$\overline{y}$=24,求出回归直线方程的系数即可求y关于x的回归方程;
(Ⅱ) 把x=1.5代入回归方程求出对应的值即可.
解答 解:(Ⅰ)由题意,$\overline{x}$=1,$\overline{y}$=24,$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n•\overline{x}•\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n•{\overline{x}}^{2}}$=$\frac{123.1-5×1×24}{5.1-5×1×1}$=31,
$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$•$\overline{x}$=24-31=-7,
∴y关于x的回归方程y=31x-7;
(Ⅱ)x=1.5时,y=39.5亿元,预测该电商2017年的销售收入39.5亿元.
点评 本题考查了线性回归直线方程的求法与应用问题,是基础题目.

练习册系列答案
相关题目
7.设向量$\overrightarrow{a}$=(2,m),$\overrightarrow{b}$=(3,-1),若$\overrightarrow{a}$⊥($\overrightarrow{a}$-2$\overrightarrow{b}$),则实数m=( )
| A. | 2或-4 | B. | 2 | C. | -$\frac{1}{4}$或$\frac{1}{2}$ | D. | -4 |
11.已知全集为R,集合A={x|x2-2x<3},B={x|x>2},则A∩(∁RB)( )
| A. | {x|-1<x<2} | B. | {x|2<x<3} | C. | {x|x<3} | D. | {x|-1<x≤2} |
12.《九章算术》卷第六《均输》中,有问题“今有竹九节,下三节容量四升,上四节容量三升.问中间二节欲均容,各多少?”其中“欲均容”的意思是:使容量变化均匀,即由下往上均匀变细.在这个问题中的中间两节容量和是( )
| A. | $1\frac{61}{66}$升 | B. | 2升 | C. | $2\frac{3}{22}$升 | D. | 3升 |
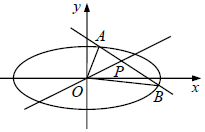 已知点P(t,$\frac{1}{2}$)在椭圆C:$\frac{{x}^{2}}{2}$+y2=1内,过P的直线l与椭圆C相交于A,B两点,且点P是线段AB的中点,O为坐标原点.
已知点P(t,$\frac{1}{2}$)在椭圆C:$\frac{{x}^{2}}{2}$+y2=1内,过P的直线l与椭圆C相交于A,B两点,且点P是线段AB的中点,O为坐标原点.