题目内容
17.若$\frac{1}{a}$<$\frac{1}{b}$<0,则下列结论正确的是( )| A. | a2>b2 | B. | 1>($\frac{1}{2}$)b>($\frac{1}{2}$)a | C. | $\frac{b}{a}$+$\frac{a}{b}$<2 | D. | aeb>bea |
分析 由题意,b<a<0,分别判断选项,即可得出结论.
解答 解:由题意,b<a<0,则a2<b2,($\frac{1}{2}$)b>($\frac{1}{2}$)a>1,$\frac{b}{a}$+$\frac{a}{b}$>2,
∵b<a<0,∴ea>eb>0,-b>-a>0
∴-bea>-aeb,∴aeb>bea,
故选D.
点评 本题考查不等式的性质,考查学生的计算能力,比较基础.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.设向量$\overrightarrow{a}$=(2,m),$\overrightarrow{b}$=(3,-1),若$\overrightarrow{a}$⊥($\overrightarrow{a}$-2$\overrightarrow{b}$),则实数m=( )
| A. | 2或-4 | B. | 2 | C. | -$\frac{1}{4}$或$\frac{1}{2}$ | D. | -4 |
5.已知f(x)=x2•ex,若函数g(x)=f2(x)-kf(x)+1恰有三个零点,则下列结论正确的是( )
| A. | k=±2 | B. | k=$\frac{8}{{e}^{2}}$ | C. | k=2 | D. | k=$\frac{4}{{e}^{2}}$+$\frac{{e}^{2}}{4}$ |
12.《九章算术》卷第六《均输》中,有问题“今有竹九节,下三节容量四升,上四节容量三升.问中间二节欲均容,各多少?”其中“欲均容”的意思是:使容量变化均匀,即由下往上均匀变细.在这个问题中的中间两节容量和是( )
| A. | $1\frac{61}{66}$升 | B. | 2升 | C. | $2\frac{3}{22}$升 | D. | 3升 |
9.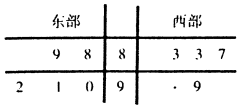 某省电视台为了解该省卫视一档成语类节目的收视情况,抽查东西两部各5个城市,得到观看该节目的人数(单位:千人)如下茎叶图所示:
某省电视台为了解该省卫视一档成语类节目的收视情况,抽查东西两部各5个城市,得到观看该节目的人数(单位:千人)如下茎叶图所示:
其中一个数字被污损.
(1)求东部各城市观看该节目观众平均人数超过西部各城市观看该节目观众平均人数的概率.
(2)随着节目的播出,极大激发了观众对成语知识的学习积累的热情,从中获益匪浅.现从观看该节目的观众中随机统计了4位观众的周均学习成语知识的时间y(单位:小时)与年龄x(单位:岁),并制作了对照表(如表所示)
由表中数据,试求线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$,并预测年龄为55岁观众周均学习成语知识时间.
参考公式:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{x}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$x.
 某省电视台为了解该省卫视一档成语类节目的收视情况,抽查东西两部各5个城市,得到观看该节目的人数(单位:千人)如下茎叶图所示:
某省电视台为了解该省卫视一档成语类节目的收视情况,抽查东西两部各5个城市,得到观看该节目的人数(单位:千人)如下茎叶图所示:其中一个数字被污损.
(1)求东部各城市观看该节目观众平均人数超过西部各城市观看该节目观众平均人数的概率.
(2)随着节目的播出,极大激发了观众对成语知识的学习积累的热情,从中获益匪浅.现从观看该节目的观众中随机统计了4位观众的周均学习成语知识的时间y(单位:小时)与年龄x(单位:岁),并制作了对照表(如表所示)
| 年龄x(岁) | 20 | 30 | 40 | 50 |
| 周均学习成语知识时间y(小时) | 2.5 | 3 | 4 | 4.5 |
参考公式:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{x}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$x.
6.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{b}$|=2|$\overrightarrow{a}$|,且($\overrightarrow{a}$+$\overrightarrow{b}$)⊥$\overrightarrow{a}$,则$\overrightarrow{a}$,$\overrightarrow{b}$的夹角等于( )
| A. | $\frac{2π}{3}$ | B. | $\frac{5π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{6}$ |
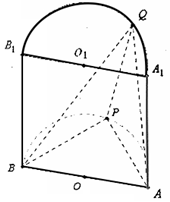 如图半圆柱OO1的底面半径和高都是1,面ABB1A1是它的轴截面(过上下底面圆心连线OO1的平面),Q,P分别是上下底面半圆周上一点.
如图半圆柱OO1的底面半径和高都是1,面ABB1A1是它的轴截面(过上下底面圆心连线OO1的平面),Q,P分别是上下底面半圆周上一点.