题目内容
已知△ABC的角A、B、C所对边的边为a，b，c，acosA=bcosB，则该三角形现状为（ ）
| A、直角三角形 |
| B、等腰三角形 |
| C、等腰直角三角形 |
| D、直角三角形或等腰三角形 |
考点：正弦定理
专题：解三角形
分析：acosA=bcosB，利用正弦定理可得sinAcosA=sinBcosB，利用倍角公式可得sin2A=sin2B，可得2A=2B或2A+2B=π，即可得出．
解答：
解：∵acosA=bcosB，
由正弦定理可得sinAcosA=sinBcosB，
∴sin2A=sin2B，
∴2A=2B或2A+2B=π，
化为A=B或A+B+
．
∴哎三角形为直角三角形或等腰三角形．
故选：D．
由正弦定理可得sinAcosA=sinBcosB，
∴sin2A=sin2B，
∴2A=2B或2A+2B=π，
化为A=B或A+B+
| π |
| 2 |
∴哎三角形为直角三角形或等腰三角形．
故选：D．
点评：本题考查了正弦定理、倍角公式、正弦函数的单调性，属于基础题．
练习册系列答案
小学课时作业全通练案系列答案
金版课堂课时训练系列答案
相关题目
已知a=log33.6，b=log93.2，c=log93.6，则（ ）
| A、a＞b＞c |
| B、a＞c＞b |
| C、b＞a＞c |
| D、c＞a＞b |
已知集合A={a+2，（a+1）2，a2+3a+3}，若1∈A，则实数a构成的集合B的元素个数是（ ）
| A、0 | B、1 | C、2 | D、3 |
已知tanα=2，则
的值为（ ）
| cos(π+2α) | ||
cos(
|
A、-
| ||
| B、1 | ||
C、
| ||
D、-
|
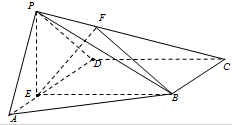如图，在四棱锥P-ABCD中，E为AD上一点，PE⊥平面ABCD，AD∥BC，AD⊥CD，BC=ED=2AE=2，EB=3，F为PC上一点，且CF=2FP．