题目内容
已知在△ABC中,边a、b、c的对角为A、B、C,A=30°,b=6,C∈[60°,120°],则此三角形中边a的取值使得函数f(x)=lg(ax2-ax+1)的值域为R的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:几何概型
专题:概率与统计
分析:由题意,首先求出三角形中a的范围以及使得函数f(x)=lg(ax2-ax+1)的值域为R的a的范围,再由几何概型的公式解答.
解答:
解:由已知在△ABC中,边a、b、c的对角为A、B、C,A=30°,b=6,C∈[60°,120°],则B∈[30°,90°],由正弦定理
=
,得到a=
=
=
∈[3,6],
使得函数f(x)=lg(ax2-ax+1)的值域为R的a的范围为
,解得a≥4,
所以由几何概型,此三角形中边a的取值使得函数f(x)=lg(ax2-ax+1)的值域为R的概率为
=
;
故选D.
| a |
| sinA |
| b |
| sinB |
| bsinA |
| sinB |
6×
| ||
| sinB |
| 3 |
| sinB |
使得函数f(x)=lg(ax2-ax+1)的值域为R的a的范围为
|
所以由几何概型,此三角形中边a的取值使得函数f(x)=lg(ax2-ax+1)的值域为R的概率为
| 6-4 |
| 6-3 |
| 2 |
| 3 |
故选D.
点评:本题考查了解三角形以及对数函数与几何概型相结合的知识,属于中档题.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
在△ABC中,a=2,b=2
,B=45°,则A等于( )
| 2 |
| A、30° |
| B、60° |
| C、60°或120° |
| D、30°或150° |
函数 f(x)=sin(ωx+φ)+b的图象如图,则 f(x)的解析式S=f(1)+f(2)+f(3)+…+f(2015)的值分别为( )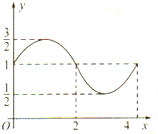

A、f(x)=
| ||||||
B、f(x)=
| ||||||
C、f(x)=
| ||||||
D、f(x)=
|
计算机执行如图的程序段后,输出的结果是( )


| A、1 | B、2 | C、3 | D、-2 |
在△ABC中,a,b,c为其三边,若(a+c)(a-c)=b(b+c),则∠A=( )
| A、60°或120° | B、60° |
| C、120° | D、150° |