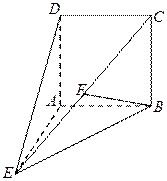题目内容
.(本小题满分14分)
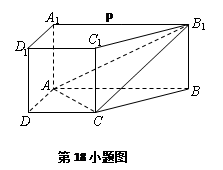
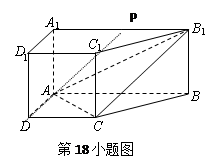
直棱柱 中,底面ABCD是直角梯形,∠BAD=∠ADC=90°,
中,底面ABCD是直角梯形,∠BAD=∠ADC=90°, .
.
(Ⅰ) 求证:AC⊥平面BB1 C1C;
C1C;
(Ⅱ)若P为A1B1的中点,求证:DP∥平面BCB1,且DP∥平面ACB1.
直棱柱
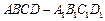 中,底面ABCD是直角梯形,∠BAD=∠ADC=90°,
中,底面ABCD是直角梯形,∠BAD=∠ADC=90°,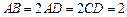 .
.(Ⅰ) 求证:AC⊥平面BB1
 C1C;
C1C;(Ⅱ)若P为A1B1的中点,求证:DP∥平面BCB1,且DP∥平面ACB1.

证明:(Ⅰ)直棱柱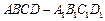 中,BB1⊥平面ABCD,
中,BB1⊥平面ABCD,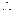 BB1⊥AC.……2分
BB1⊥AC.……2分
又 ∠BAD=∠ADC=90°,
∠BAD=∠ADC=90°,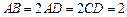 ,
,
∴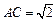 ,∠CAB=45°,∴
,∠CAB=45°,∴ ,
,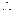 BC⊥AC.………… 5分[
BC⊥AC.………… 5分[
又 ,
,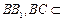 平面BB1C1C,
平面BB1C1C, AC⊥平面BB1C1C.…………7分
AC⊥平面BB1C1C.…………7分
 (Ⅱ)证明:由P为A1B1的中点,有PB1‖AB,且PB1=
(Ⅱ)证明:由P为A1B1的中点,有PB1‖AB,且PB1=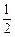 AB.…………2分
AB.…………2分
又∵DC‖AB,DC=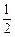 AB,
AB,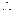 DC ∥PB1,且DC= PB1,…4分
DC ∥PB1,且DC= PB1,…4分
∴DC B1P为平行四边形,从而CB1∥DP.
又CB1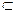 面ACB1,DP
面ACB1,DP 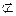 面ACB1,
面ACB1,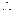 DP‖面ACB1…6分
DP‖面ACB1…6分
同理,DP‖面BCB1. …………7分
(注:第(Ⅰ)问7分,第(Ⅱ)问7分)
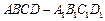 中,BB1⊥平面ABCD,
中,BB1⊥平面ABCD,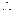 BB1⊥AC.……2分
BB1⊥AC.……2分又
 ∠BAD=∠ADC=90°,
∠BAD=∠ADC=90°,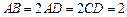 ,
,∴
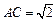 ,∠CAB=45°,∴
,∠CAB=45°,∴ ,
,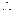 BC⊥AC.………… 5分[
BC⊥AC.………… 5分[又
 ,
,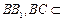 平面BB1C1C,
平面BB1C1C,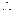 AC⊥平面BB1C1C.…………7分
AC⊥平面BB1C1C.…………7分 (Ⅱ)证明:由P为A1B1的中点,有PB1‖AB,且PB1=
(Ⅱ)证明:由P为A1B1的中点,有PB1‖AB,且PB1=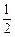 AB.…………2分
AB.…………2分又∵DC‖AB,DC=
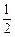 AB,
AB,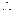 DC ∥PB1,且DC= PB1,…4分
DC ∥PB1,且DC= PB1,…4分∴DC B1P为平行四边形,从而CB1∥DP.
又CB1
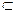 面ACB1,DP
面ACB1,DP 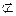 面ACB1,
面ACB1,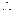 DP‖面ACB1…6分
DP‖面ACB1…6分同理,DP‖面BCB1. …………7分
(注:第(Ⅰ)问7分,第(Ⅱ)问7分)
略

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
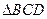 中,
中, ,
,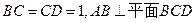 ,
,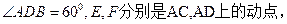 且
且
 为何值,总有
为何值,总有
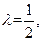 求三棱锥
求三棱锥 的体积.
的体积. 侧棱与底面垂直,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点.
侧棱与底面垂直,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点.
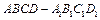 中,M、N、P、Q分别为AD、CD、
中,M、N、P、Q分别为AD、CD、 、
、 的中点.
的中点.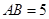 ,AA1=4,.点D是AB的中点.
,AA1=4,.点D是AB的中点.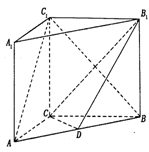
 的平面角的正切值.
的平面角的正切值.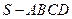 中,底面
中,底面 为矩形,平面
为矩形,平面
 底面
底面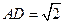 ,
,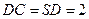 ,
,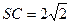 ,点
,点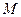 是侧棱
是侧棱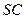 的中点.
的中点.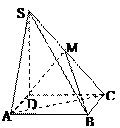
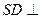 平面
平面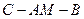 的大小.
的大小.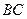 求一点
求一点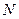 ,使点
,使点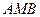 的距离为
的距离为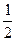 .
. 面ABCD,
面ABCD,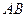 ∥
∥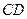 ,AD=CD=1,∠
,AD=CD=1,∠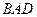 =120°,
=120°,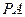 =
=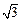 ,∠
,∠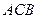 =90°,M是线段PD上的一点(不包括端点).
=90°,M是线段PD上的一点(不包括端点).
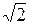 的正方形,E为P
的正方形,E为P C的中点,PB=PD.
C的中点,PB=PD.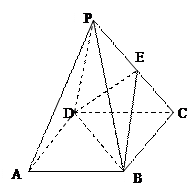
 如图,正方形
如图,正方形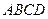 所在平面与
所在平面与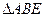 所在平面垂直,
所在平面垂直,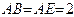 ,
,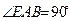 ,
,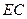 中点为
中点为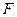 .
.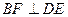
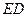 与平面
与平面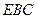 所成角
所成角