题目内容
不等式组
表示的平面区域是三角形,则a的取值范围是( )
|
| A、a≥0或-10<a≤-6 |
| B、-10<a≤-6 |
| C、-10<a<-6 |
| D、a≥0 |
考点:二元一次不等式(组)与平面区域
专题:不等式的解法及应用
分析:作出不等式组
对应的平面区域,根据平面区域是三角形,确定直线截距的取值范围即可,进而解得a的取值范围.
|
解答:
解:先作出不等式组
对应的平面区域如图(阴影部分):
不等式x-3y-a≤0,表示直线x-3y-a=0的上方,
由
,解得
,即B(5,5),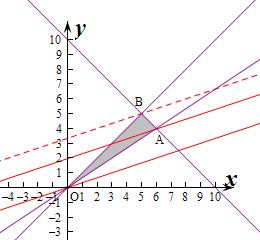
若直线x-3y-a=0经过B时,解得a=-10,
由
,解得
,即A(6,4),
若直线x-3y-a=0经过A时,解得a=-6,
若直线x-3y-a=0经过原点时,解得a=0,
由图象可知a的取值范围是a≥0或-10<a≤-6,
故选:A
|
不等式x-3y-a≤0,表示直线x-3y-a=0的上方,
由
|
|

若直线x-3y-a=0经过B时,解得a=-10,
由
|
|
若直线x-3y-a=0经过A时,解得a=-6,
若直线x-3y-a=0经过原点时,解得a=0,
由图象可知a的取值范围是a≥0或-10<a≤-6,
故选:A
点评:本题主要考查二元一次不等式组表示平面区域的知识,利用数形结合是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在△ABC中,M是BC的中点,AM=4,BC=10,则
•
=( )
| AB |
| AC |
| A、9 | B、-9 | C、21 | D、-21 |
若f(x)=|log3x|,则满足不等式f(x)>f(
)的x的范围是( )
| 7 |
| 2 |
A、(0,
| ||||
B、(
| ||||
C、(0,
| ||||
D、(
|
双曲线
-y2=1的一个焦点坐标是( )
| x2 |
| 4 |
A、(-
| ||
| B、(-2,0) | ||
C、(
| ||
| D、(1,0) |
已知点P是双曲线
-
=1(a>0,b>0)左支上一点,F1,F2是双曲线的左右两个焦点,且
•
=0,线段PF2的垂直平分线恰好是该双曲线的一条渐近线,则离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| PF1 |
| PF2 |
A、
| ||
B、
| ||
| C、2 | ||
D、
|
已知向量
=(3,x),
=(8,12),且
⊥
,则实数x的值为( )
| a |
| b |
| a |
| b |
| A、-2 | ||
| B、2 | ||
C、-
| ||
D、
|
在棱长为a的正方体ABCD-A1B1C1D1中,若点P是棱上一点,则满足PA+PC1=2a的点P的个数为( )
| A、3个 | B、4个 |
| C、5 个 | D、6个 |
在△ABC中,a,b,c分别是角A,B,C的对边,若b=2c•cosA,则△ABC一定是( )
| A、等边三角形 |
| B、等腰三角形 |
| C、直角三角形 |
| D、钝角三角形 |