题目内容
5.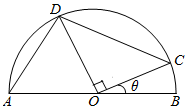 如图,在半径r=8的半圆中,O是圆心,AB是直径,C、D在半圆上滑动,且CO⊥OD.
如图,在半径r=8的半圆中,O是圆心,AB是直径,C、D在半圆上滑动,且CO⊥OD.(1)设∠BOC=θ,试将四边形ABCD的面积表示为θ的函数;
(2)求当θ为何值时,面积S有最大值,最大值是多少?
分析 (1)利用三角形的面积公式,可将四边形ABCD的面积表示为θ的函数;
(2)利用辅助角公式化简,即可求出θ为何值时,面积S有最大值及最大值.
解答 解:(1)由题意,∠BOC=θ,∠COD=90°,∠AOD=90°-θ,
∴四边形ABCD的面积S=$\frac{1}{2}×8×8×sinθ$+$\frac{1}{2}×8×8$+$\frac{1}{2}×8×8×sin(90°-θ)$=32(1+sinθ+cosθ)(0°<θ<90°);
(2)S=32(1+sinθ+cosθ)=32+32$\sqrt{2}$sin(θ+45°),
∴θ=45°时,面积S有最大值,最大值是32+32$\sqrt{2}$.
点评 本题考查三角形面积的计算,考查辅助角公式,考查学生的计算能力,正确球场面积是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.已知条件p:x≥1,条件q:$\frac{1}{x}$<1,则¬p是q的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
14.如果ξ是1个离散型随机变量,那么下列命题中假命题是( )
| A. | ξ取每个可能值的概率是非负数 | |
| B. | ξ取所有可能值的概率之和为1 | |
| C. | ξ取某2个可能值的概率等于分别取其中这2个值的概率之和 | |
| D. | ξ的取值只能是正整数 |