题目内容
15.求函数y=2sin(x+$\frac{π}{3}$)的单调递增区间.分析 将z=x+$\frac{π}{3}$,求y=2sinz的单调递减区间,解得x的取值.
解答 解:y=2sin(x+$\frac{π}{3}$),
设z=x+$\frac{π}{3}$,
∴2kπ+$\frac{π}{2}$≤z≤2kπ+$\frac{π}{2}$,k∈Z,y=2sinz的单调递减,
2kπ+$\frac{π}{2}$≤x+$\frac{π}{3}$≤2kπ+$\frac{π}{2}$,k∈Z,
2kπ+$\frac{π}{6}$≤x≤2kπ+$\frac{7}{6}π$,
函数y=2sin(x+$\frac{π}{3}$)的单调递增区间[2kπ+$\frac{π}{6}$,2kπ+$\frac{7}{6}π$].
点评 本题考查正弦函数的单调性,属于基础题.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
1.下列命题中错误的是( )
| A. | 圆柱的轴截面是过母线的截面中面积最大的一个 | |
| B. | 圆锥的轴截面是所在过顶点的截面中面积最大的一个 | |
| C. | 圆台的所有平行于底面的截面都是圆面 | |
| D. | 圆锥所有的轴截面是全等的等腰三角形 |
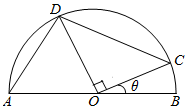 如图,在半径r=8的半圆中,O是圆心,AB是直径,C、D在半圆上滑动,且CO⊥OD.
如图,在半径r=8的半圆中,O是圆心,AB是直径,C、D在半圆上滑动,且CO⊥OD.