题目内容
已知直线l:
(t为参数,α为l的倾斜角),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C为:ρ2-6ρcosθ+5=0.
(1)若直线l与曲线C相切,求α的值;
(2)设曲线C上任意一点的直角坐标为(x,y),求x+y的取值范围.
|
(1)若直线l与曲线C相切,求α的值;
(2)设曲线C上任意一点的直角坐标为(x,y),求x+y的取值范围.
考点:简单曲线的极坐标方程,参数方程化成普通方程
专题:坐标系和参数方程
分析:(1)求出圆的直角坐标方程,直线的直角坐标方程,利用直线l与曲线C相切,列出关系式,即可求α的值;
(2)曲线C上任意一点的直角坐标为(x,y),通过圆的参数方程,得到x+y的表达式,利用三角函数化简,即可求解取值范围.
(2)曲线C上任意一点的直角坐标为(x,y),通过圆的参数方程,得到x+y的表达式,利用三角函数化简,即可求解取值范围.
解答:
解:(1)曲线C的直角坐标方程为x2+y2-6x+5=0
即(x-3)2+y2=4曲线C为圆心为(3,0),半径为2的圆.
直线l的方程为:xsinα-ycosα+sinα=0…(3分)
∵直线l与曲线C相切∴
=2
即sinα=
…(5分)
∵α∈[0,π)∴α=
或
…(6分)
(2)设x=3+2cosθ,y=2sinθ
则 x+y=3+2cosθ+2sinθ=3+2
sin(θ+
)…(9分)
∴x+y的取值范围是[3-2
,3+2
].…(10分)
即(x-3)2+y2=4曲线C为圆心为(3,0),半径为2的圆.
直线l的方程为:xsinα-ycosα+sinα=0…(3分)
∵直线l与曲线C相切∴
| |3sinα+sinα| | ||
|
即sinα=
| 1 |
| 2 |
∵α∈[0,π)∴α=
| π |
| 6 |
| 5π |
| 6 |
(2)设x=3+2cosθ,y=2sinθ
则 x+y=3+2cosθ+2sinθ=3+2
| 2 |
| π |
| 4 |
∴x+y的取值范围是[3-2
| 2 |
| 2 |
点评:本题考查直线与圆的参数方程以及极坐标方程的应用,直线与圆的位置关系,三角函数的化简求值,考查计算能力.

练习册系列答案
相关题目
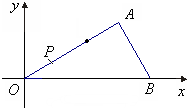 如图,在平面直角坐标系中,△AOB是直角三角形,∠AOB=30°,∠A=90°,OB=12,点P在OA上,且OP=2
如图,在平面直角坐标系中,△AOB是直角三角形,∠AOB=30°,∠A=90°,OB=12,点P在OA上,且OP=2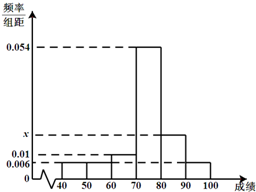 某班50位学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[40,50)、[50,60)、[60,70)、[70,80)、[80,90)、[90,100].
某班50位学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[40,50)、[50,60)、[60,70)、[70,80)、[80,90)、[90,100].