题目内容
极坐标方程ρsin2θ-2•cosθ=0表示的曲线是 ．
考点：简单曲线的极坐标方程
专题：坐标系和参数方程
分析：先将原极坐标方程两边同乘以ρ后化成直角坐标方程，再利用直角坐标方程进行判断．
解答：
解：原极坐标方程ρsin2θ-2•cosθ=0化为：
ρ2sin2θ-2•ρcosθ=0，
∴y2-2x=0，它表示抛物线，
故答案为：方程为y2=2x的抛物线．
ρ2sin2θ-2•ρcosθ=0，
∴y2-2x=0，它表示抛物线，
故答案为：方程为y2=2x的抛物线．
点评：本题考查点的极坐标和直角坐标的互化，能在极坐标系中用极坐标刻画点的位置，体会在极坐标系和平面直角坐标系中刻画点的位置的区别，能进行极坐标和直角坐标的互化．
练习册系列答案
时刻准备着暑假作业原子能出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
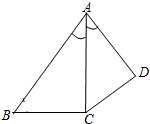在平面四边形ABCD中，AD=1，CD=2，AB=3，cos∠CAD=