题目内容
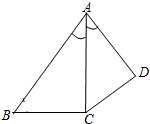 在平面四边形ABCD中,AD=1,CD=2,AB=3,cos∠CAD=
在平面四边形ABCD中,AD=1,CD=2,AB=3,cos∠CAD=2
| ||
| 7 |
(1)求AC的长;
(2)若cos∠BAD=-
| ||
| 14 |
考点:正弦定理
专题:计算题,解三角形
分析:(1)在△ACD中,由已知及余弦定理即可解得AC的值;
(2)先求cos∠CAD,cos∠BAD,sin∠CAD,sin∠BAD的值,从而可求sin∠BAC,即可求出S△ABC的值.
(2)先求cos∠CAD,cos∠BAD,sin∠CAD,sin∠BAD的值,从而可求sin∠BAC,即可求出S△ABC的值.
解答:
解:(1)∵在△ACD中,由余弦定理知:CD2=AD2+AC2-2AD•AC•cos∠CAD,
∴4=1+AC2-×AC×
,
∴可解得:AC=
或-
(舍去),
(2)∵cos∠CAD=
,cos∠BAD=-
,
∴sin∠CAD=
,sin∠BAD=
,
∵sin∠BAC=sin(∠BAD-∠CAD)=sin∠BADcos∠CAD-cos∠BADsin∠CAD=
×
+
×
=
,
∴S△ABC=
×AB×AC×sin∠BAC=
×3×
×
=
.
∴4=1+AC2-×AC×
2
| ||
| 7 |
∴可解得:AC=
| 7 |
3
| ||
| 7 |
(2)∵cos∠CAD=
2
| ||
| 7 |
| ||
| 14 |
∴sin∠CAD=
| ||
| 7 |
3
| ||
| 14 |
∵sin∠BAC=sin(∠BAD-∠CAD)=sin∠BADcos∠CAD-cos∠BADsin∠CAD=
3
| ||
| 14 |
2
| ||
| 7 |
| ||
| 14 |
| ||
| 7 |
| ||
| 2 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 7 |
| ||
| 2 |
3
| ||
| 4 |
点评:本题主要考察了正弦定理、三角形面积公式的应用,属于基本知识的考查.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目