题目内容
6.已知cosα=$\frac{\sqrt{5}}{5}$且tanα>0.(1)求tanα的值;
(2)求$\frac{cosα+2sin(π-α)}{sin(\frac{π}{2}-α)-sinα}$的值.
分析 (1)由已知先利用同角三角函数关系式求出sinα,再求出tanα的值.
(2)利用诱导公式求解.
解答 解:(1)∵cosα=$\frac{\sqrt{5}}{5}$且tanα>0,
∴sinα=$\sqrt{1-(\frac{\sqrt{5}}{5})^{2}}$=$\frac{2\sqrt{5}}{5}$,
∴tanα=$\frac{sinα}{cosα}$=$\frac{\frac{2\sqrt{5}}{5}}{\frac{\sqrt{5}}{5}}$=2.
(2)∵cosα=$\frac{\sqrt{5}}{5}$,sin$α=\frac{2\sqrt{5}}{5}$,
∴$\frac{cosα+2sin(π-α)}{sin(\frac{π}{2}-α)-sinα}$=$\frac{cosα+2sinα}{cosα-sinα}$=$\frac{\frac{\sqrt{5}}{5}+2×\frac{2\sqrt{5}}{5}}{\frac{\sqrt{5}}{5}-\frac{2\sqrt{5}}{5}}$=-5.
点评 本题考查三角函数值的求法,是基础题,解题时要认真审题,注意诱导公式和同角三角函数关系式的合理运用.

练习册系列答案
相关题目
14.已知等比数列{an}的前n项和为Sn,则下列一定成立的是( )
| A. | 若a4>0,则a2016<0 | B. | 若a5>0,则a2015<0 | ||
| C. | 若a4>0,则S2016>0 | D. | 若a5>0,则S2015>0 |
11.设实数x>1,则$\frac{{x}^{2}-2x+2}{2x-2}$的最小值为( )
| A. | 2 | B. | 3 | C. | 1 | D. | $\frac{1}{2}$ |
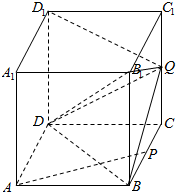 如图,正方体ABCD-A1B1C1D1的棱长为2,P是BC的中点,点Q是棱CC1上的动点.
如图,正方体ABCD-A1B1C1D1的棱长为2,P是BC的中点,点Q是棱CC1上的动点.