题目内容
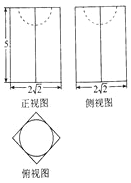
17．如图是某几何体的三视图，俯视图是边长为2的正三角形，则该几何体的体积是$2\sqrt{3}$
分析 三视图复原的几何体是三棱柱截去一个三棱锥，剩余一个四棱锥的几何体．
解答 解：三视图复原的几何体是三棱柱截去一个三棱锥，剩余一个四棱锥的几何体，
可得几何体的体积为：$\frac{2}{3}×\frac{1}{2}×2×\sqrt{3}×3$=2$\sqrt{3}$．
故答案为：$2\sqrt{3}$．
点评 本题考查了三棱柱、三棱锥、四棱锥的三视图、体积计算公式，考查了推理能力与计算能力，属于中档题．
练习册系列答案
应用题作业本系列答案
相关题目
12．若某空间几何体的三视图如图所示，则该几何体的表面积是（ ）
| A． | 48+π | B． | 48-π | C． | 48+2π | D． | 48-2π |
2．如图，已知$\overrightarrow{AB}$=a，$\overrightarrow{AC}$=b，$\overrightarrow{BD}$=3 $\overrightarrow{DC}$，用$\vec a$，$\vec b$表示$\overrightarrow{AD}$，则$\overrightarrow{AD}$=（ ）
| A． | $\vec a$+$\frac{3}{4}$$\vec b$ | B． | $\frac{1}{4}$ $\vec a$+$\frac{3}{4}$$\vec b$ | C． | $\frac{1}{4}$ $\vec a$+$\frac{1}{4}$$\vec b$ | D． | $\frac{3}{4}$ $\vec a$+$\frac{1}{4}$$\vec b$ |
