题目内容
在△ABC中，AC=2，BC=6，已知点O是△ABC内一点，且满足
+3
+4
=
，则
•(
+2
)= ．
| OA |
| OB |
| OC |
| 0 |
| OC |
| BA |
| BC |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：由于
=
+
，
=
+
，满足
+3
+4
=
，可得
=-
(
+3
)．再利用数量积运算性质即可得出．
| OA |
| OC |
| CA |
| OB |
| OC |
| CB |
| OA |
| OB |
| OC |
| 0 |
| OC |
| 1 |
| 8 |
| CA |
| CB |
解答：
解：∵
=
+
，
=
+
，满足
+3
+4
=
，
∴
+
+3(
+
)+4
=
，
∴
=-
(
+3
)．
∵
+2
=
-
+2
=
-3
．
∴
•(
+2
)=-
(
+3
)•(
-3
)
=-
(
2-9
2)
=-
(22-62)
=40．
故答案为：40．
| OA |
| OC |
| CA |
| OB |
| OC |
| CB |
| OA |
| OB |
| OC |
| 0 |
∴
| OC |
| CA |
| OC |
| CB |
| OC |
| 0 |
∴
| OC |
| 1 |
| 8 |
| CA |
| CB |
∵
| BA |
| BC |
| CA |
| CB |
| BC |
| CA |
| CB |
∴
| OC |
| BA |
| BC |
| 1 |
| 8 |
| CA |
| CB |
| CA |
| CB |
=-
| 1 |
| 8 |
| CA |
| CB |
=-
| 1 |
| 8 |
=40．
故答案为：40．
点评：本题考查了向量的运算法则、数量积运算性质，考查了推理能力与计算能力，属于难题．
练习册系列答案
阅读快车系列答案
相关题目
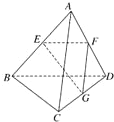如图，已知空间四边形ABCD的每条边及AC、BD的长都为a，点E、F、G分别是AB、AD、DC的中点，求：
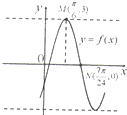如图，函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜