题目内容
“若g′（x0）=0，则x0是函数y=g（x）的极值点，因为g（x）=x3中，g′（x）=3x2且g′（0）=0，所以0是g（x）=x3的极值点．”在此“三段论”中，下列说法正确的是（ ）
| A、推理过程错误 |
| B、大前提错误 |
| C、小前提错误 |
| D、大、小前提错误 |
考点：演绎推理的基本方法
专题：简易逻辑
分析：在使用三段论推理证明中，如果命题是错误的，则可能是“大前提”错误，也可能是“小前提”错误，也可能是推理形式错误，分析的其大前提的形式：“对于可导函数f（x），如果g'（x0）=0，那么x=x0是函数g（x）的极值点”，不难得到结论．
解答：
解：对于可导函数g（x），如果g'（x0）=0，且满足当x＞x0时和当x＜x0时的导函数值异号时，那么x=x0是函数g（x）的极值点，
而大前提是：“对于可导函数g（x），如果g'（x0）=0，那么x=x0是函数g（x）的极值点”，不是真命题，
∴大前提错误，
故选B．
而大前提是：“对于可导函数g（x），如果g'（x0）=0，那么x=x0是函数g（x）的极值点”，不是真命题，
∴大前提错误，
故选B．
点评：本题考查的知识点是演绎推理的基本方法，演绎推理是一种必然性推理，演绎推理的前提与结论之间有蕴涵关系．因而，只要前提是真实的，推理的形式是正确的，那么结论必定是真实的，但错误的前提可能导致错误的结论．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
函数y=sin2x的一个单调区间是（ ）
A、[-
| ||||
B、[-
| ||||
C、[
| ||||
D、[
|
已知向量
=（-1，2），
=（x，4），且
∥
，则x的值为（ ）
| a |
| b |
| a |
| b |
| A、8 | B、2 | C、-2 | D、-8 |
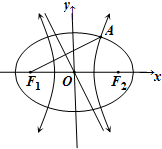如图，F1，F2是椭圆C1：| x2 |
| m2 |
| y2 |
| n2 |
| x2 |
| a2 |
| y2 |
| b2 |
| 1 | ||
|
| 1 | ||
|
| A、2 | ||
B、
| ||
C、
| ||
| D、4 |
已知p：∅⊆{0}；q：{1}∈{1，2}．由它们构成的以下三个命题中，真命题有（ ）
①p∧q ②p∨q ③￢p．
①p∧q ②p∨q ③￢p．
| A、1个 | B、2个 | C、3个 | D、0个 |