题目内容
设实数x,y满足约束条件
,则u=
的取值范围是 .
|
| 2x+y |
| x+2y |
考点:简单线性规划
专题:不等式的解法及应用
分析:u=
=
,设k=
,利用数形结合即可得到结论.
| 2x+y |
| x+2y |
2+
| ||
1+2×
|
| y |
| x |
解答:
解:u=
=
,设k=
,
则u=
=
=
=
+
,
作出不等式组对应的平面区域如图:则k的几何意义为区域内的点到原点的斜率,
由图象可知OA的斜率最大,OB的斜率最小,
由
,解得
,即A(1,2),此时k=2,
由
,解得
,即B(3,1),此时k=
,
则
≤k≤2,
则
≤u≤
,
故u=
的取值范围是[
,
],
故答案为:[
,
]
| 2x+y |
| x+2y |
2+
| ||
1+2×
|
| y |
| x |

则u=
2+
| ||
1+2×
|
| 2+k |
| 1+2k |
| ||||
| 1+2k |
| 1 |
| 2 |
| ||
| 1+2k |
作出不等式组对应的平面区域如图:则k的几何意义为区域内的点到原点的斜率,
由图象可知OA的斜率最大,OB的斜率最小,
由
|
|
由
|
|
| 1 |
| 3 |
则
| 1 |
| 3 |
则
| 4 |
| 5 |
| 7 |
| 5 |
故u=
| 2x+y |
| x+2y |
| 4 |
| 5 |
| 7 |
| 5 |
故答案为:[
| 4 |
| 5 |
| 7 |
| 5 |
点评:本题主要考查线性规划的应用以及直线斜率的求解,利用数形结合是解决本题的关键.

练习册系列答案
相关题目
甲乙两名运动员在某项测试中的8次成绩如茎叶图所示,则甲运动员的极差与乙运动员的众数分别是( )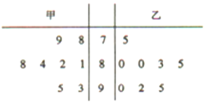

| A、20、80 |
| B、20、81 |
| C、17、80 |
| D、17、81 |
将分针拨慢5分钟,则分钟转过的弧度数是( )
A、
| ||
B、-
| ||
C、
| ||
D、
|
函数f(x)满足对定义域内的任意x,都有f(x+2)+f(x)<2f(x+1),则函数f(x)可以是( )
| A、f(x)=2x+1 |
| B、f(x)=x2-2x |
| C、f(x)=ex |
| D、f(x)=lnx |
已知cos(
+φ)=-
,且角φ的终边上有一点(2,a)则a=( )
| π |
| 2 |
| ||
| 2 |
A、-
| ||
B、2
| ||
C、±2
| ||
D、
|

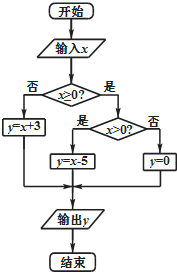 执行如图所示的程序框图,在集合A={x∈R|-10≤x≤10}中随机地取一个数值作为x输入,则输出的y值落在区间(-5,3)内的概率为( )
执行如图所示的程序框图,在集合A={x∈R|-10≤x≤10}中随机地取一个数值作为x输入,则输出的y值落在区间(-5,3)内的概率为( )