题目内容
12.矩形区域 ABCD 中,AB 长为 2 千米,BC 长为 1 千米,在 A 点和 C 点处各有一个通信基站,其覆盖范围均为方圆 1 千米,若在该矩形区域内随意选取一地点,则该地点无信号的概率为1-$\frac{π}{4}$.分析 根据题意,算出扇形区域ADE和扇形区域CBF的面积之和为$\frac{π}{2}$,结合矩形ABCD的面积为2,可得在矩形ABCD内且没有信号的区域面积为2-$\frac{π}{2}$,再用几何概型计算公式即可算出所求的概率.
解答  解:∵如图,扇形ADE的半径为1,圆心角等于90°,
解:∵如图,扇形ADE的半径为1,圆心角等于90°,
∴扇形ADE的面积为S1=$\frac{1}{4}$×π×12=$\frac{π}{4}$,
同理可得,扇形CBF的在,面积S2=$\frac{π}{4}$,
又∵长方形ABCD的面积S=2×1=2,
∴在该矩形区域内随机地选一地点,则该地点无信号的概率是P=$\frac{2-\frac{π}{2}}{2}$=1-$\frac{π}{4}$,
故答案为:1-$\frac{π}{4}$.
点评 本题着重考查了几何概型及其计算方法的知识,属于基础题.

练习册系列答案
相关题目
2.下列说法正确的是( )
| A. | 若直线l1与l2斜率相等,则l1∥l2 | |
| B. | 若直线l1∥l2,则k1=k2 | |
| C. | 若直线l1,l2的斜率不存在,则l1∥l2 | |
| D. | 若两条直线的斜率不相等,则两直线不平行 |
17.已知x,y的值如表所示,如果y与x呈线性相关且回归直线方程为$\widehat{y}$=$\widehat{b}$x+2,则$\widehat{b}$=( )
| x | 2 | 3 | 4 |
| y | 5 | 4 | 6 |
| A. | 3 | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
4.设y=f(x)为定义在R上的可导函数,定义运算⊕和?如下:对任意m,n∈R均有m⊕n=|f(m)|•n;m?n=f'(m)+n.若存在a∈R,使得对于任意x∈R,恒有a⊕x=a?x=x成立,则称实数a为函数的基元,则下列函数中恰有两个基元的是( )
| A. | f(x)=x2+1 | B. | $f(x)=\frac{1}{2}({x^3}-3x)$ | C. | f(x)=2x3+3x2 | D. | f(x)=cosx |
5.从点(2,3)射出的光线沿斜率k=$\frac{1}{2}$的方向射到y轴上,则反射光线所在的直线方程为( )
| A. | x+2y-4=0 | B. | 2x+y-1=0 | C. | x+6y-16=0 | D. | 6x+y-8=0 |
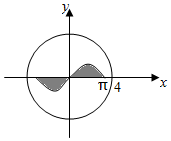 如图,圆O:x2+y2=16内的正弦曲线y=sinx,x∈[-π,π]与x轴围成的区域记为M(图中阴影部分),随机向圆O内投一个点P,记A表示事件“点P落在一象限”,B表示事件“点P落在区域M内”,则概率P(B|A)=$\frac{1}{2π}$.
如图,圆O:x2+y2=16内的正弦曲线y=sinx,x∈[-π,π]与x轴围成的区域记为M(图中阴影部分),随机向圆O内投一个点P,记A表示事件“点P落在一象限”,B表示事件“点P落在区域M内”,则概率P(B|A)=$\frac{1}{2π}$.