题目内容
3.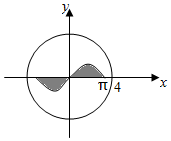 如图,圆O:x2+y2=16内的正弦曲线y=sinx,x∈[-π,π]与x轴围成的区域记为M(图中阴影部分),随机向圆O内投一个点P,记A表示事件“点P落在一象限”,B表示事件“点P落在区域M内”,则概率P(B|A)=$\frac{1}{2π}$.
如图,圆O:x2+y2=16内的正弦曲线y=sinx,x∈[-π,π]与x轴围成的区域记为M(图中阴影部分),随机向圆O内投一个点P,记A表示事件“点P落在一象限”,B表示事件“点P落在区域M内”,则概率P(B|A)=$\frac{1}{2π}$.
分析 利用定积分求出阴影的面积,得出P(A),P(AB),再利用条件概率公式计算.
解答 解:圆O的面积为16π,
阴影部分的面积为S=2${∫}_{0}^{π}$sinxdx=-2cosx${|}_{0}^{π}$=4,
∴P(AB)=$\frac{2}{16π}$=$\frac{1}{8π}$,P(A)=$\frac{1}{4}$,
∴P(B|A)=$\frac{P(AB)}{P(A)}$=$\frac{1}{2π}$.
故答案为:$\frac{1}{2π}$.
点评 本题考查了条件概率的计算,属于基础题.

练习册系列答案
相关题目
13.已知函数f(x)=x2-m是定义在区间[-3-m,m2-m]上的奇函数,则( )
| A. | f(m)<f(1) | B. | f(m)>f(1) | ||
| C. | f(m)=-f(1) | D. | f(m)与f(1)大小不能确定 |
18.某同学投篮命中率为0.6,则该同学1次投篮时命中次数X的期望为( )
| A. | 0.4 | B. | 0.36 | C. | 0.16 | D. | 0.6 |
15. 如图,一辆汽车在一条水平的公路上向正西行驶,到A处测得公路北侧一山顶D在西偏北30°(即∠BAC=30°)的方向上;行驶600m后到达B处,测得此山顶在西偏北75°(即∠CBE=75°)的方向上,且仰角为30°.则此山的高度CD=( )
如图,一辆汽车在一条水平的公路上向正西行驶,到A处测得公路北侧一山顶D在西偏北30°(即∠BAC=30°)的方向上;行驶600m后到达B处,测得此山顶在西偏北75°(即∠CBE=75°)的方向上,且仰角为30°.则此山的高度CD=( )
 如图,一辆汽车在一条水平的公路上向正西行驶,到A处测得公路北侧一山顶D在西偏北30°(即∠BAC=30°)的方向上;行驶600m后到达B处,测得此山顶在西偏北75°(即∠CBE=75°)的方向上,且仰角为30°.则此山的高度CD=( )
如图,一辆汽车在一条水平的公路上向正西行驶,到A处测得公路北侧一山顶D在西偏北30°(即∠BAC=30°)的方向上;行驶600m后到达B处,测得此山顶在西偏北75°(即∠CBE=75°)的方向上,且仰角为30°.则此山的高度CD=( )| A. | $100\sqrt{6}$m | B. | $100\sqrt{3}$m | C. | $300\sqrt{6}$m | D. | $150\sqrt{3}$m |