题目内容
19.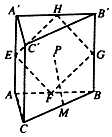 如图直三棱柱ABC-A'B'C'中,△ABC为边长为2的等边三角形,AA'=4,点E、F、G、H、M分别是边AA'、AB、BB'、A'B'、BC的中点,动点P在四边形EFGH内部运动,并且始终有MP∥平面ACC'A',则动点P的轨迹长度为( )
如图直三棱柱ABC-A'B'C'中,△ABC为边长为2的等边三角形,AA'=4,点E、F、G、H、M分别是边AA'、AB、BB'、A'B'、BC的中点,动点P在四边形EFGH内部运动,并且始终有MP∥平面ACC'A',则动点P的轨迹长度为( )| A. | 2 | B. | 2π | C. | $2\sqrt{3}$ | D. | 4 |
分析 利用平面与平面平行,推出直线与平面平行,得到P的轨迹,然后求解动点P的轨迹长度.
解答  解:连结HF,FM,HM,因为直三棱柱ABC-A'B'C'中,点E、F、G、H、M分别是边AA'、AB、BB'、A'B'、BC的中点,可知HF∥AA′,FM∥AC,HF∩FM=F,可知平面HFM∥平面ACC'A',P∈有平面HFM,
解:连结HF,FM,HM,因为直三棱柱ABC-A'B'C'中,点E、F、G、H、M分别是边AA'、AB、BB'、A'B'、BC的中点,可知HF∥AA′,FM∥AC,HF∩FM=F,可知平面HFM∥平面ACC'A',P∈有平面HFM,
所以有MP∥平面ACC'A',可得P的轨迹是线段HF,HF=4.
故选:D.
点评 本题考查空间几何体的特征,平面与平面平行的判定定理以及性质定理的应用,轨迹的判断,考查计算能力空间想象能力.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
10.已知圆${x^2}+{y^2}+mx-\frac{1}{4}=0$与抛物线$y=\frac{1}{4}{x^2}$的准线相切,则m=( )
| A. | $±2\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | $±\sqrt{3}$ |
7.将三个标有A,B,C的小球随机放入编号为1,2,3,4的四个盒子中,则1号盒子内没有球的不同放法的总数为( )
| A. | 27 | B. | 37 | C. | 64 | D. | 81 |
4.已知命题p:?x0∈R,lnx0≥x0-1.命题q:?θ∈R,sinθ+cosθ<1,.则下列命题中为真命题的是( )
| A. | p∧q | B. | (¬p)∧q | C. | (¬p)∧(¬q) | D. | p∧(¬q) |
8.某计算器有两个数据输入口M1,M2一个数据输出口N,当M1,M2分别输入正整数1时,输出口N输出2,当M1输入正整数m1,M2输入正整数m2时,N的输出是n;当M1输入正整数m1,M2输入正整数m2+1时,N的输出是n+5;当M1输入正整数m1+1,MM2输入正整数m2时,N的输出是n+4.则当M1输入60,M2输入50时,N的输出是( )
| A. | 494 | B. | 492 | C. | 485 | D. | 483 |
9.已知函数f(x)=sin(ωx+2φ)-2sinφcos(ωx+φ)(ω>0,φ∈R)在(π,$\frac{3π}{2}$)上单调递减,则ω的取值范围是( )
| A. | (0,2] | B. | (0,$\frac{1}{2}$] | C. | [$\frac{1}{2}$,1] | D. | [$\frac{1}{2}$,$\frac{5}{4}$] |