题目内容
7．将三个标有A，B，C的小球随机放入编号为1，2，3，4的四个盒子中，则1号盒子内没有球的不同放法的总数为（ ）| A． | 27 | B． | 37 | C． | 64 | D． | 81 |
分析 根据题意，要求1号盒子内没有球，即三个小球全部放进2、3、4号盒子，进而分析A，B，C的小球放进小盒的情况数目，有分步计数原理计算可得答案．
解答 解：根据题意，要求1号盒子内没有球，即三个小球全部放进2、3、4号盒子，
分析可得：A球可以放进三个盒子中任意1个，即有3种选择方法；
同理，B、C球也有3种选择方法，
则不同的放法有3×3×3=27种；
故选：A．
点评 本题考查分步计数原理的运用，解题的关键在于转化问题，即转化为将三个小球全部放进2、3、4号盒子的问题．
练习册系列答案
相关题目
2．已知抛物线y2=4x的焦点F与椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的一个焦点重合，它们在第一象限内的交点为P，且PF与x轴垂直，则椭圆的离心率为（ ）
| A． | $\sqrt{3}-\sqrt{2}$ | B． | $\sqrt{2}-1$ | C． | $\frac{1}{2}$ | D． | $\frac{\sqrt{2}}{2}$ |
18．已知函数$f（x）=\left\{\begin{array}{l}{x^2}+（{a+1}）x+2a，（{x＞0}）\\{log_a}（{x+1}）+1，（{-1＜x≤0}）\end{array}\right.$，（a＜0，a≠1），若函数y=|f（x）|在$[{-\frac{1}{3}，+∞}）$上单调递增，且关于x的方程|f（x）|=x+3恰有两个不同的实根，则a的取值范围为（ ）
| A． | $[{\frac{3}{2}，2}）$ | B． | $（{1，\frac{3}{2}}]∪\left\{{2，6}\right\}$ | C． | {2，6} | D． | $[{\frac{3}{2}，\frac{5}{3}}]$ |
2．若圆x2+y2-2x-2y=0上至少有三个不同点到直线l：y=kx的距离为$\frac{{\sqrt{2}}}{2}$，则直线l的倾斜角的取值范围是（ ）
| A． | [15°，45°] | B． | [15°，75°] | C． | [30°，60°] | D． | [0°，90°] |
19．
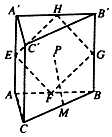如图直三棱柱ABC-A'B'C'中，△ABC为边长为2的等边三角形，AA'=4，点E、F、G、H、M分别是边AA'、AB、BB'、A'B'、BC的中点，动点P在四边形EFGH内部运动，并且始终有MP∥平面ACC'A'，则动点P的轨迹长度为（ ）
如图直三棱柱ABC-A'B'C'中，△ABC为边长为2的等边三角形，AA'=4，点E、F、G、H、M分别是边AA'、AB、BB'、A'B'、BC的中点，动点P在四边形EFGH内部运动，并且始终有MP∥平面ACC'A'，则动点P的轨迹长度为（ ）| A． | 2 | B． | 2π | C． | $2\sqrt{3}$ | D． | 4 |
16．侧面都是直角三角形的正三棱锥，底面边长为a时，该三棱锥的全面积是（ ）
| A． | $\frac{3+\sqrt{3}}{4}$a2 | B． | $\frac{3}{4}$a2 | C． | $\frac{3+\sqrt{3}}{2}$a2 | D． | $\frac{6+\sqrt{3}}{4}$a2 |
17．已知sinθ＞0且cosθ＜0，则角θ的终边所在的象限是（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |