题目内容
14.已知函数$f(x)=\frac{1}{2}x-\frac{1}{2}$,若对于数列{an}满足:an+1=4f(an)-an-1+4(n∈N*,n≥2),且a1=-1,a2=2.(1)求证:数列{an-an-1}(n∈N*,n≥2)为等差数列,并求数列{an}的通项公式;
(2)设${b_n}=\frac{{{a_n}+2}}{n}×{3^{n-1}}$,若数列{bn}的前n项和为Sn,求Sn.
分析 (1)由已知$f(x)=\frac{1}{2}x-\frac{1}{2}$及an+1=4f(an)-an-1+4,可得(an+1-an)-(an-an-1)=2(n≥2),求出a2-a1=3,可得数列{an+1-an}是一个以3为首项,以2为公差的等差数列;再由等差数列的通项公式可得an+1-an=2n+1,然后利用累加法求得数列{an}的通项公式;
(2)把(1)中求得的通项公式代入${b_n}=\frac{{{a_n}+2}}{n}×{3^{n-1}}$,然后利用错位相减法求Sn.
解答 (1)证明:由题意,${a_{n+1}}=4f({a_n})-{a_{n-1}}+4=4(\frac{1}{2}{a_n}-\frac{1}{2})-{a_{n-1}}+4=2{a_n}-{a_{n-1}}+2(n≥2)$,
即(an+1-an)-(an-an-1)=2(n≥2),
∵a1=-1,a2=2,∴a2-a1=3,
∴数列{an+1-an}是一个以3为首项,以2为公差的等差数列;
则an+1-an=3+2(n-1)=2n+1,
则a2-a1=2×1+1,a3-a2=2×2+1,…,an-an-1=2(n-1)+1(n≥2).
累加得${a_n}={a_1}+2[1+2+…+(n-1)]+(n-1)={n^2}-2$.
验证n=1时上式成立,∴${a_n}={n^2}-2$;
(2)解:${b_n}=\frac{{{a_n}+2}}{n}=\frac{{{n^2}-2+2}}{n}×{3^{n-1}}=n×{3^{n-1}}$,
则${S_n}={b_1}+{b_2}+…+{b_n}=1×{3^0}+2×{3^1}+3×{3^2}+…+n×{3^{n-1}}$,
$3{S_n}=1×{3^1}+2×{3^2}+3×{3^3}+…+n×{3^n}$,
两式作差得:$-2{S_n}=1×{3^0}+1×{3^1}+1×{3^2}+…+1×{3^{n-1}}-n×{3^n}=\frac{{1-{3^n}}}{1-3}-n×{3^n}=\frac{{1-{3^n}}}{-2}-n×{3^n}$.
∴${S_n}=\frac{{1-{3^n}}}{4}+\frac{n}{2}×{3^n}=\frac{{(2n-1)×{3^n}+1}}{4}$.
点评 本题考查数列递推式,考查等差关系的确定,训练了错位相减法求数列的前n项和,是中档题.

| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
| A. | [-1.1] | B. | (-2,1] | C. | (-2,+∞) | D. | (-1,1] |
| A. | [15°,45°] | B. | [15°,75°] | C. | [30°,60°] | D. | [0°,90°] |
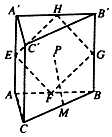 如图直三棱柱ABC-A'B'C'中,△ABC为边长为2的等边三角形,AA'=4,点E、F、G、H、M分别是边AA'、AB、BB'、A'B'、BC的中点,动点P在四边形EFGH内部运动,并且始终有MP∥平面ACC'A',则动点P的轨迹长度为( )
如图直三棱柱ABC-A'B'C'中,△ABC为边长为2的等边三角形,AA'=4,点E、F、G、H、M分别是边AA'、AB、BB'、A'B'、BC的中点,动点P在四边形EFGH内部运动,并且始终有MP∥平面ACC'A',则动点P的轨迹长度为( )| A. | 2 | B. | 2π | C. | $2\sqrt{3}$ | D. | 4 |
| A. | (1,2),4 | B. | (1,-2),2 | C. | (-1,2),2 | D. | (1,-2),4 |
| 分数区间 | [50,70] | [70,90] | [90,110] | [110,130] | [130,150] |
| 人数 | 2 | 8 | 32 | 38 | 20 |
(2)现从成绩在[70,110)中按照分数段,采取分成抽样的方法随机抽取5人,再在这5人中随机抽取2人作小题得分分析,求恰有1人的成绩在[70,90)上的概率.