题目内容
8.某计算器有两个数据输入口M1,M2一个数据输出口N,当M1,M2分别输入正整数1时,输出口N输出2,当M1输入正整数m1,M2输入正整数m2时,N的输出是n;当M1输入正整数m1,M2输入正整数m2+1时,N的输出是n+5;当M1输入正整数m1+1,MM2输入正整数m2时,N的输出是n+4.则当M1输入60,M2输入50时,N的输出是( )| A. | 494 | B. | 492 | C. | 485 | D. | 483 |
分析 依题记f(m1,m2)=f(m1,m2-1)+5×1=f(m1,1)+5×(m2-1)=f(m1-1,1)+4×1+5×(m2-1)=…=f(1,1)+4×(m1-1)+5×f(m1,1),将m1=60,m2=50,f(1,1)=2,代入得结论.
解答 解:依题记f(m1,m2)=f(m1,m2-1)+5×1=f(m1,1)+5×(m2-1)
=f(m1-1,1)+4×1+5×(m2-1)=…=f(1,1)+4×(m1-1)+5×(m2-1),
将m1=60,m2=50,f(1,1)=2,代入得483.
故选D.
点评 本题考查学生通过观察、归纳、抽象出数列的规律的能力,要求学生首先分析题意,找到规律,并进行推导得出答案.

练习册系列答案
相关题目
18.已知函数$f(x)=\left\{\begin{array}{l}{x^2}+({a+1})x+2a,({x>0})\\{log_a}({x+1})+1,({-1<x≤0})\end{array}\right.$,(a<0,a≠1),若函数y=|f(x)|在$[{-\frac{1}{3},+∞})$上单调递增,且关于x的方程|f(x)|=x+3恰有两个不同的实根,则a的取值范围为( )
| A. | $[{\frac{3}{2},2})$ | B. | $({1,\frac{3}{2}}]∪\left\{{2,6}\right\}$ | C. | {2,6} | D. | $[{\frac{3}{2},\frac{5}{3}}]$ |
19.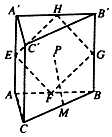 如图直三棱柱ABC-A'B'C'中,△ABC为边长为2的等边三角形,AA'=4,点E、F、G、H、M分别是边AA'、AB、BB'、A'B'、BC的中点,动点P在四边形EFGH内部运动,并且始终有MP∥平面ACC'A',则动点P的轨迹长度为( )
如图直三棱柱ABC-A'B'C'中,△ABC为边长为2的等边三角形,AA'=4,点E、F、G、H、M分别是边AA'、AB、BB'、A'B'、BC的中点,动点P在四边形EFGH内部运动,并且始终有MP∥平面ACC'A',则动点P的轨迹长度为( )
 如图直三棱柱ABC-A'B'C'中,△ABC为边长为2的等边三角形,AA'=4,点E、F、G、H、M分别是边AA'、AB、BB'、A'B'、BC的中点,动点P在四边形EFGH内部运动,并且始终有MP∥平面ACC'A',则动点P的轨迹长度为( )
如图直三棱柱ABC-A'B'C'中,△ABC为边长为2的等边三角形,AA'=4,点E、F、G、H、M分别是边AA'、AB、BB'、A'B'、BC的中点,动点P在四边形EFGH内部运动,并且始终有MP∥平面ACC'A',则动点P的轨迹长度为( )| A. | 2 | B. | 2π | C. | $2\sqrt{3}$ | D. | 4 |
16.侧面都是直角三角形的正三棱锥,底面边长为a时,该三棱锥的全面积是( )
| A. | $\frac{3+\sqrt{3}}{4}$a2 | B. | $\frac{3}{4}$a2 | C. | $\frac{3+\sqrt{3}}{2}$a2 | D. | $\frac{6+\sqrt{3}}{4}$a2 |
3.已知圆C:(x+1)2+(y-2)2=4,则其圆心和半径分别为( )
| A. | (1,2),4 | B. | (1,-2),2 | C. | (-1,2),2 | D. | (1,-2),4 |
20.命题“?x∈[0,+∞],x3+x≥0”的否定是( )
| A. | ?x∈(-∞,0),x3+x<0 | B. | ?x∈(-∞,0),x3+x≥0 | ||
| C. | $?{x_0}∈[0,\;+∞),\;x_0^3+{x_0}<0$ | D. | $?{x_0}∈[0,\;+∞),\;x_0^3+{x_0}≥0$ |
17.已知sinθ>0且cosθ<0,则角θ的终边所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
18.设点P(x,y)在△ABC的内部及其边界上运动,其中A(1,1),B(2,4),C(3,1),则$\frac{y}{x}$的取值范围是( )
| A. | [$\frac{1}{3}$,+∞) | B. | [2,+∞) | C. | ($\frac{1}{3}$,2) | D. | [$\frac{1}{3}$,2] |