题目内容
logx+1（2x2+3x-5）＞2的解集是 ．
考点：指、对数不等式的解法
专题：函数的性质及应用
分析：根据对数的运算将原不等式化为：logx+1（2x2+3x-5）＞logx+1（x+1）2，再对底数分类讨论，利用对数函数的单调性、底数、真数的条件，分别列出不等式组求出x的范围，最后并在一起．
解答：
解：原不等式可化为：logx+1（2x2+3x-5）＞logx+1（x+1）2，
当x+1＞1时，则
，解得x＞2；
当0＜x+1＜1时，则
，解得x∈∅，
综上得，不等式的解集是{x|x＞2}，
故答案为：{x|x＞2}．
当x+1＞1时，则
|
当0＜x+1＜1时，则
|
综上得，不等式的解集是{x|x＞2}，
故答案为：{x|x＞2}．
点评：本题考查利用对数函数的单调性求对数不等式，注意底数、真数的限制条件，考查分类讨论思想和计算能力，属于中档题．
练习册系列答案
相关题目
下列函数中，在区间（0，5）上为增函数的是（ ）
A、y=
| ||
| B、y=x2+3 | ||
| C、y=9-x | ||
| D、y=-|x| |
设a=log35，b=log34，c=log22，则（ ）
| A、a＞b＞c |
| B、c＞a＞b |
| C、b＞a＞c |
| D、b＞c＞a |
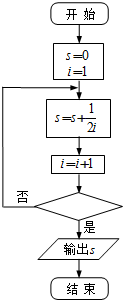如图给出的是计算| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| 20 |
| A、i＞8？ | B、i＞9？ |
| C、i＞10？ | D、i＞11？ |