题目内容
设函数f（x）=ax（a＞0且a≠1），f（2）=9，则f（
）=（ ）
| 1 |
| 2 |
A、
| ||
| B、3 | ||
C、
| ||
D、
|
考点：函数的值
专题：函数的性质及应用
分析：由函数f（x）=ax（a＞0且a≠1）满足f（2）=9，可求a，从而可求得f（
）．
| 1 |
| 2 |
解答：
解：∵f（x）=ax（a＞0且a≠1）满足f（2）=a2=9，
∴a=3．
∴f（x）=3x，
∴f（
）=
．
故选：D．
∴a=3．
∴f（x）=3x，
∴f（
| 1 |
| 2 |
| 3 |
故选：D．
点评：本题考查数指数函数的解析式，着重考查指数函数的概念与应用，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
某班学生体检中检查视力的结果如表，从表中可以看出，全班视力数据的众数是（ ）
| 视力 | 0.5以下 | 0.7 | 0.8 | 0.9 | 1.0 | 1.0以上 |
| 占全班人数百分比 | 2% | 6% | 3% | 20% | 65% | 4% |
| A、0.9 | B、1.0 |
| C、20% | D、65% |
在2点至3点之间的某一时刻，分针与时针分别在钟面上“2”字的两侧，而且与“2”字的距离相等，这一时刻是（ ）
A、2时6
| ||
B、2时7
| ||
C、2时8
| ||
D、2时9
|
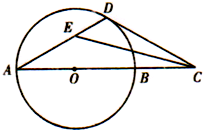如图所示，在圆的直径AB的延长线上任取一点C，过点C作圆的切线CD，切点为D，∠ACD的平分线交AD于点E，则∠CED