题目内容
7.设F1、F2是椭圆$\frac{{x}^{2}}{4}$+y2=1的左右焦点,过F2的直线l与椭圆交于A,B两点,求△F1AB的最大值.分析 由椭圆方程求出右焦点坐标,设直线l的方程为x=ty+$\sqrt{3}$,联立直线方程和椭圆方程,化为关于y的一元二次方程,利用根与系数的关系求出${y}_{1}+{y}_{2}=\frac{-2\sqrt{3}t}{{t}^{2}+4},{y}_{1}{y}_{2}=\frac{-1}{{t}^{2}+4}$,代入三角形面积公式后整理,然后利用基本不等式求最值.
解答 解:由椭圆方程$\frac{{x}^{2}}{4}$+y2=1,得a2=4,b2=1,
∴c=$\sqrt{{a}^{2}-{b}^{2}}$=$\sqrt{3}$,则F2($\sqrt{3}$,0).
设直线l的方程为x=ty+$\sqrt{3}$,
联立$\left\{\begin{array}{l}{x=ty+\sqrt{3}}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$,得$({t}^{2}+4){y}^{2}+2\sqrt{3}ty-1=0$,
设A(x1,y1),B(x2,y2),
则${y}_{1}+{y}_{2}=\frac{-2\sqrt{3}t}{{t}^{2}+4},{y}_{1}{y}_{2}=\frac{-1}{{t}^{2}+4}$,
∴${S}_{△{F}_{1}AB}=\frac{1}{2}×2\sqrt{3}|{y}_{1}-{y}_{2}|$=$\sqrt{3}\sqrt{(\frac{-2\sqrt{3}t}{{t}^{2}+4})^{2}+\frac{4}{{t}^{2}+4}}$
=$4\sqrt{3}\sqrt{\frac{{t}^{2}+1}{{t}^{4}+8{t}^{2}+16}}$=$4\sqrt{3}\sqrt{\frac{1}{6+(1+{t}^{2})+\frac{9}{1+{t}^{2}}}}$$≤4\sqrt{3}\sqrt{\frac{1}{6+2\sqrt{9}}}=2$.
当且仅当1+t2=3,即$t=±\sqrt{2}$时,△F1AB的面积取得最大值2.
点评 本题考查椭圆的方程和性质,主要考查椭圆的方程的运用,联立直线方程,运用韦达定理,同时考查基本不等式的运用,属于中档题.

 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案| A. | 6 | B. | 5 | C. | $\frac{5}{3}$ | D. | -$\frac{5}{3}$ |
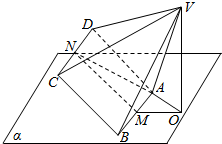 如图,底面为正方形且各侧棱长均相等的四棱锥V-ABCD可绕着棱AB任意旋转,若AB?平面α,M、N分别是AB、CD的中点,AB=2,VA=$\sqrt{5}$,点V在平面α上的射影为点O,则当ON的最大时,二面角C-AB-O的大小是( )
如图,底面为正方形且各侧棱长均相等的四棱锥V-ABCD可绕着棱AB任意旋转,若AB?平面α,M、N分别是AB、CD的中点,AB=2,VA=$\sqrt{5}$,点V在平面α上的射影为点O,则当ON的最大时,二面角C-AB-O的大小是( )| A. | 90° | B. | 105° | C. | 120° | D. | 135° |
| x | 2 | 3 | 5 | 6 |
| y | 7 | 8-a | 9+a | 12 |
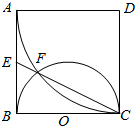 如图,正方形ABCD边长为2,以D为圆心、DA为半径的圆弧与以BC为直径的半圆O交于点F,连结CF并延长交AB于点E.
如图,正方形ABCD边长为2,以D为圆心、DA为半径的圆弧与以BC为直径的半圆O交于点F,连结CF并延长交AB于点E.