题目内容
19.已知集合D=$\left\{{(x,y)\left|{\frac{x^2}{4}+\frac{y^2}{3}=1}\right.}\right\}$,有下面四个命题:p1:?(x,y)∈D,$\sqrt{{{(x-1)}^2}+{y^2}}$≥3 p2:?(x,y)∈D,$\sqrt{{{(x-1)}^2}+{y^2}}$<1
p3:?(x,y)∈D,$\sqrt{{{(x-1)}^2}+{y^2}}$<4 p4:?(x,y)∈D,$\sqrt{{{(x-1)}^2}+{y^2}}$≥2
其中的真命题是( )
| A. | p1,p3 | B. | p1,p4 | C. | p2,p3 | D. | p2,p4 |
分析 集合D=$\left\{{(x,y)\left|{\frac{x^2}{4}+\frac{y^2}{3}=1}\right.}\right\}$表示焦点在x轴上,长轴长为4,短轴长为2$\sqrt{3}$的椭圆,$\sqrt{{{(x-1)}^2}+{y^2}}$表示椭圆上的点到(1,0)点的距离,进而得到答案.
解答 解:集合D=$\left\{{(x,y)\left|{\frac{x^2}{4}+\frac{y^2}{3}=1}\right.}\right\}$表示焦点在x轴上,长轴长为4,短轴长为2$\sqrt{3}$的椭圆,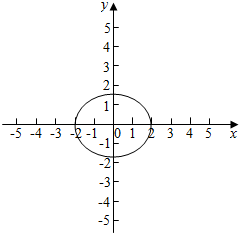
$\sqrt{{{(x-1)}^2}+{y^2}}$表示椭圆上的点到(1,0)点的距离d,
则d∈[1,3],
故p1:?(x,y)∈D,$\sqrt{{{(x-1)}^2}+{y^2}}$≥3,为真命题,
p2:?(x,y)∈D,$\sqrt{{{(x-1)}^2}+{y^2}}$<1,为假命题,
p3:?(x,y)∈D,$\sqrt{{{(x-1)}^2}+{y^2}}$<4,为真命题,
p4:?(x,y)∈D,$\sqrt{{{(x-1)}^2}+{y^2}}$≥2,为假命题,
故p1,p3是真命题,
故选:A.
点评 本题考查的知识点是椭圆的标准方程,两点之间的距离公式,全称命题和特称命题,难度中档.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案
相关题目
11.用秦九韶算法求多项式f(x)=4x4+3x3+2x2+x+7的值,则f(2)的值为( )
| A. | 98 | B. | 105 | C. | 112 | D. | 119 |
9.复数$\frac{2-i}{1-i}$的共轭复数是( )
| A. | $\frac{3+i}{2}$ | B. | $\frac{1-i}{2}$ | C. | $\frac{3-i}{2}$ | D. | $\frac{-3-i}{2}$ |
 如图,一个棱长为2的正方体沿其棱的中点截去部分后所得几何体的三视图如图所示,则该几何体的体积为$\frac{23}{3}$.
如图,一个棱长为2的正方体沿其棱的中点截去部分后所得几何体的三视图如图所示,则该几何体的体积为$\frac{23}{3}$.