题目内容
17.轴截面是边长等于2的等边三角形的圆锥,它的体积等于$\frac{\sqrt{3}}{3}$π.分析 由轴截面是边长等于2的等边三角形,求出圆锥的底面半径,母线长,进而求出圆锥的底面周长,代入圆锥体积公式,即可求出圆锥的体积.
解答 解:一个圆锥的轴截面(过旋转轴的截面)是边长为2的等边三角形,
所以圆锥的母线为l=2;底面半径为r=1;圆锥的高为:$\sqrt{3}$.
所以圆锥的体积为:$\frac{1}{3}$×$\sqrt{3}$×π•12=$\frac{\sqrt{3}}{3}$π,
故答案为:$\frac{\sqrt{3}}{3}$π.
点评 本题是基础题,考查圆锥的轴截面知识,圆锥的表面积的求法,实际上这个圆锥又叫等边圆锥,需要同学注意它的边角关系,常考题目.

练习册系列答案
相关题目
2.将3个半径为1的球和一个半径为$\sqrt{2}-1$的球叠为两层放在桌面上,上层只放一个较小的球,四个球两两相切,那么上层小球的最高点到桌面的距离是( )
| A. | $\frac{{3\sqrt{2}+\sqrt{6}}}{3}$ | B. | $\frac{{\sqrt{3}+2\sqrt{6}}}{3}$ | C. | $\frac{{\sqrt{2}+2\sqrt{6}}}{3}$ | D. | $\frac{{2\sqrt{2}+\sqrt{6}}}{3}$ |
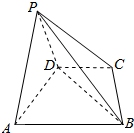 在四棱锥P-ABCD 中,△PAD 为等边三角形,底面ABCD为等腰梯形,满足AB∥CD,AD=DC=$\frac{1}{2}$AB=2,且平面PAD⊥平面ABCD.
在四棱锥P-ABCD 中,△PAD 为等边三角形,底面ABCD为等腰梯形,满足AB∥CD,AD=DC=$\frac{1}{2}$AB=2,且平面PAD⊥平面ABCD.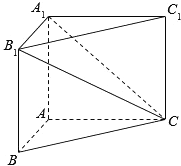 直三棱柱ABC-A1B1C1的底面是等腰直角三角形,AB=AC=2,四棱锥C-ABB1A1的体积等于4.
直三棱柱ABC-A1B1C1的底面是等腰直角三角形,AB=AC=2,四棱锥C-ABB1A1的体积等于4. 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2,PD=AD=1,PD⊥底面ABCD.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2,PD=AD=1,PD⊥底面ABCD.