题目内容
2.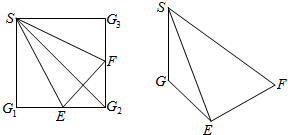 如图,正方形SG1G2G3中,E,F分别是G1G2,G2G3的中点,现沿SE,SF及EF把这个正方形折成一个四面体,使G1,G2,G3三点重合,重合后的点记为G,则在四面体S-EFG中.
如图,正方形SG1G2G3中,E,F分别是G1G2,G2G3的中点,现沿SE,SF及EF把这个正方形折成一个四面体,使G1,G2,G3三点重合,重合后的点记为G,则在四面体S-EFG中.(1)求证:SG⊥平面EFG;
(2)请指出四面体S-EFG中有哪些平面互相垂直;
(3)若M,N分别是SF,GE的中点,求异面直线MN与SE所成角的余弦值.
分析 (1)折成四面体S-EFG后,SG⊥GE,SG⊥GF,由此能证明SG⊥平面EFG.
(2)面SGE⊥面GEF,面SGE⊥面GEF,面SGE⊥面SGF.
(3)取EF的中点A,连结AM,AN,则∠AMN为异面直线MN与SE所成的角,由此利用余弦定理能求出异面直线MN与SE所成角的余弦值.
解答 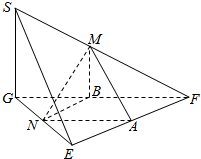 证明:(1)∵在折前正方形SG1G2G3中,
证明:(1)∵在折前正方形SG1G2G3中,
SG1⊥G1E,SG3⊥G3F,
∴折成四面体S-EFG后,SG⊥GE,SG⊥GF,
又∵GE∩GF=G,∴SG⊥平面EFG.
解:(2)∵SG⊥平面EFG,SG?平面SGE,SG?平面SGF,
∴面SGE⊥面GEF,面SGE⊥面GEF,
∵SG⊥GF,SG⊥GE,GF⊥GE,∴面SGE⊥面SGF.
(3)取EF的中点A,连结AM,AN,
∵M是SF的中点,∴MA∥SE,
∴∠AMN为异面直线MN与SE所成的角,
设正方形边长为2a,
又MA=$\frac{1}{2}SE=\frac{\sqrt{5}}{2}a$,AN=$\frac{1}{2}a$,
取GF中点B,在Rt△MBN中,MN=$\frac{\sqrt{6}}{2}a$,
在△MNA中,cos∠AMN=$\frac{M{N}^{2}+M{A}^{2}-N{A}^{2}}{2MN•MA}$=$\frac{\sqrt{30}}{6}$.
∴异面直线MN与SE所成角的余弦值为$\frac{\sqrt{30}}{6}$.
点评 本题考查线面垂直的证明,考查面面垂直的判断,考查异面直线所成角的余弦值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
12.在正方体ABCD-A1B1C1D1中,点P为正方形A1B1C1D1内部及边上的动点,且BD⊥平面AA1P,则直线BP与AD1所成角θ的取值范围是( )
| A. | 0<θ≤$\frac{π}{3}$ | B. | 0<θ≤$\frac{π}{2}$ | C. | 0≤θ≤$\frac{π}{3}$ | D. | 0≤θ≤$\frac{π}{2}$ |
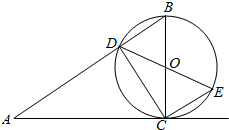 如图,BC是圆O的直径,过C作圆O的切线AC,连接AB交圆O于点D.
如图,BC是圆O的直径,过C作圆O的切线AC,连接AB交圆O于点D.