题目内容
11.设G是三角形ABC的重心,已知A(x1,y1),B(x2,y2),C(x3,y3),则G点的坐标为($\frac{{x}_{1}{+x}_{2}{+x}_{3}}{3}$,$\frac{{y}_{1}{+y}_{2}{+y}_{3}}{3}$).分析 根据题意,画出图形,结合图形,利用BC的中点D的坐标和向量相等,求出G点的坐标.
解答 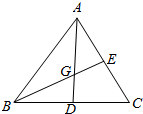 解:如图所示,G是△ABC的重心,A(x1,y1),B(x2,y2),C(x3,y3),
解:如图所示,G是△ABC的重心,A(x1,y1),B(x2,y2),C(x3,y3),
设G(x,y),则BC的中点D的坐标为($\frac{{x}_{2}{+x}_{3}}{2}$,$\frac{{y}_{2}{+y}_{3}}{2}$);
又$\overrightarrow{AG}$=(x-x1,y-y1),$\overrightarrow{GD}$=($\frac{{x}_{2}{+x}_{3}}{2}$-x,$\frac{{y}_{2}{+y}_{3}}{2}$-y),
且$\overrightarrow{AG}$=2$\overrightarrow{GD}$,
∴$\left\{\begin{array}{l}{x{-x}_{1}={(x}_{2}{+x}_{3})-2x}\\{y{-y}_{1}={(y}_{2}{+y}_{3})-2y}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=\frac{{x}_{1}{+x}_{2}{+x}_{3}}{3}}\\{y=\frac{{y}_{1}{+y}_{2}{+y}_{3}}{3}}\end{array}\right.$;
∴G点的坐标为($\frac{{x}_{1}{+x}_{2}{+x}_{3}}{3}$,$\frac{{y}_{1}{+y}_{2}{+y}_{3}}{3}$).
故答案为:($\frac{{x}_{1}{+x}_{2}{+x}_{3}}{3}$,$\frac{{y}_{1}{+y}_{2}{+y}_{3}}{3}$).
点评 本题考查了求三角形重心坐标的应用问题,是基础题目.

| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
| A. | 30° | B. | 38° | C. | 45° | D. | 60° |
| A. | $\frac{2n+2}{{n}^{2}}$ | B. | $\frac{n+5}{3n}$ | C. | $\frac{2n+2}{3n}$ | D. | $\frac{2n+2}{2n+3}$ |
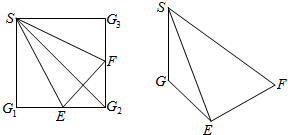 如图,正方形SG1G2G3中,E,F分别是G1G2,G2G3的中点,现沿SE,SF及EF把这个正方形折成一个四面体,使G1,G2,G3三点重合,重合后的点记为G,则在四面体S-EFG中.
如图,正方形SG1G2G3中,E,F分别是G1G2,G2G3的中点,现沿SE,SF及EF把这个正方形折成一个四面体,使G1,G2,G3三点重合,重合后的点记为G,则在四面体S-EFG中.