题目内容
14.双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦点分别为F1,F2,过F1作圆:x2+y2=$\frac{3}{4}$c2的切线交双曲线左右支分别于A,B两点,且|$\overrightarrow{BA}$|=|$\overrightarrow{B{F}_{2}}$|,则双曲线的离心率等于$\frac{\sqrt{13}+1}{2}$.分析 由题意,设直线的斜率为$\sqrt{3}$,直线的倾斜角为60°,利用过F1作圆:x2+y2=$\frac{3}{4}$c2的切线交双曲线左右支分别于A,B两点,且|$\overrightarrow{BA}$|=|$\overrightarrow{B{F}_{2}}$|,可得|AF1|=2a,求出A(a-c,$\sqrt{3}$a),代入双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1可得e的方程,即可得结论.
解答 解:由题意,设直线的斜率为$\sqrt{3}$,直线的倾斜角为60°,
∵过F1作圆:x2+y2=$\frac{3}{4}$c2的切线交双曲线左右支分别于A,B两点,且|$\overrightarrow{BA}$|=|$\overrightarrow{B{F}_{2}}$|,
∴|AF1|=2a,
∴A(a-c,$\sqrt{3}$a),
代入双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1可得$\frac{(a-c)^{2}}{{a}^{2}}-\frac{3{a}^{2}}{{b}^{2}}$=1,
∴(e2-1)(e2-2e)=3
可得e=$\frac{\sqrt{13}+1}{2}$.
故答案为:$\frac{\sqrt{13}+1}{2}$.
点评 本题考查直线与圆的位置关系,考查直线与双曲线的位置关系,考查双曲线的性质,属于中档题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
5.已知函数f(x)的图象如图所示,则f(x)的解析式可能是( )
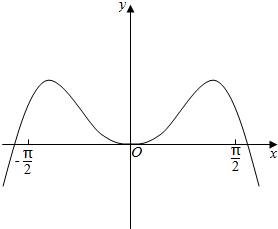

| A. | x2cosx | B. | sinx2 | C. | xsinx | D. | x2-$\frac{1}{6}$x4 |
19.设一直棱柱的底面是边长为2$\sqrt{2}$正方形,棱柱的顶点都在同一个球面上,且这个球面的表面积为64π,则该四棱柱的对角线与底面成的角是( )
| A. | 30° | B. | 38° | C. | 45° | D. | 60° |
6.数列{an}中an=$\frac{1}{{n}^{2}}$(n∈N*),f(n)=(1-a3)(1-a4)…(1-an),f(n)=( )
| A. | $\frac{2n+2}{{n}^{2}}$ | B. | $\frac{n+5}{3n}$ | C. | $\frac{2n+2}{3n}$ | D. | $\frac{2n+2}{2n+3}$ |
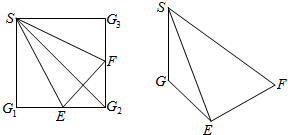 如图,正方形SG1G2G3中,E,F分别是G1G2,G2G3的中点,现沿SE,SF及EF把这个正方形折成一个四面体,使G1,G2,G3三点重合,重合后的点记为G,则在四面体S-EFG中.
如图,正方形SG1G2G3中,E,F分别是G1G2,G2G3的中点,现沿SE,SF及EF把这个正方形折成一个四面体,使G1,G2,G3三点重合,重合后的点记为G,则在四面体S-EFG中.