题目内容
2.已知函数f(x)=$\left\{\begin{array}{l}{sinx,x≥1}\\{{e}^{x},x<1}\end{array}\right.$.(1)若f(x)≥1,求x的取值范围;
(2)求函数f(x)的值域.
分析 (1)讨论当x≥1时,sinx=1,解得x=2kπ+$\frac{π}{2}$,k∈N;再由x<1时,解不等式ex≥1,即可得到所求x的取值范围;
(2)分别讨论x≥1时,x<1时,结合正弦函数和指数函数的值域,即可得到所求f(x)的值域.
解答 解:(1)当x≥1时,sinx≥1,
但sinx≤1,即有sinx=1,
解得x=2kπ+$\frac{π}{2}$,k∈Z,即为x=2kπ+$\frac{π}{2}$,k∈N;
当x<1时,ex≥1,可得x≥0,即为0≤x<1.
综上可得x的取值范围是[0,1)∪{x|x=2kπ+$\frac{π}{2}$,k∈N};
(2)当x≥1时,f(x)=sinx∈[-1,1];
当x<1时,f(x)=ex∈(0,e).
可得f(x)的值域为[-1,1]∪(0,e)=[-1,e).
点评 本题考查分段函数的运用:解不等式和求函数的值域,注意运用三角函数的值域和指数函数的值域和单调性,考查运算能力,属于中档题.

练习册系列答案
相关题目
7.对空间任一点O和不共线三点A,B,C,能得到P,A,B,C四点共面的是( )
| A. | $\overrightarrow{OP}$=$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$ | B. | $\overrightarrow{OP}$=$\frac{1}{3}$$\overrightarrow{OA}$+$\frac{1}{3}$$\overrightarrow{OB}$+$\frac{1}{3}$$\overrightarrow{OC}$ | ||
| C. | $\overrightarrow{OP}$=-$\overrightarrow{OA}$+$\frac{1}{2}$$\overrightarrow{OB}$+$\frac{1}{2}$$\overrightarrow{OC}$ | D. | 以上皆错 |
14.设集合M={y|y=2x,x∈R},N={x|y=loga(x+1),a>0,a≠1},则M和N的关系是( )
| A. | M?N | B. | M?N | C. | M=N | D. | M∩N=∅ |
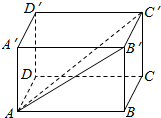 如图,长方体ABCD-A′B′C′D′中,化简下列各式,并在图中标出化简得到的向量:
如图,长方体ABCD-A′B′C′D′中,化简下列各式,并在图中标出化简得到的向量: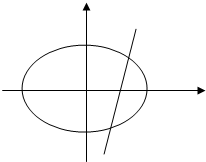 已知椭圆:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左右焦点分别为F1(-1,0),F2(1,0),且过点$(-1,\frac{3}{2})$,右顶点为A,经过点F2的动直线l与椭圆交于B,C两点.
已知椭圆:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左右焦点分别为F1(-1,0),F2(1,0),且过点$(-1,\frac{3}{2})$,右顶点为A,经过点F2的动直线l与椭圆交于B,C两点.