题目内容

8．方程x2+y2+4mx-2y+5m=0表示圆，应该有m＜$\frac{1}{4}$，或m＞1．

分析 方程x2+y2+Dx+Ey+F=0表示圆，则D2+E2-4F＞0，进而得到答案．

解答 解：若方程x2+y2+4mx-2y+5m=0表示圆，
则（4m）2+（-2）2-4×5m＞0，
即4m2-5m+1＞0，
解得：m＜$\frac{1}{4}$，或m＞1，
故答案为：m＜$\frac{1}{4}$，或m＞1．

点评 本题考查的知识点是圆的一般方程，正确理解方程x2+y2+Dx+Ey+F=0表示圆的充要条件，是解答的关键．

练习册系列答案
相关题目
18．已知函数$f（x）=\left\{\begin{array}{l}{3^x}，x＜1\\-x，x≥1\end{array}\right.$，则f（f（1））=$\frac{1}{3}$；若f（x）=2，则x=log32．
19．设{an}为等差数列，Sn表示前n项之和，其中a1+a2=0，且S3=3，求该数列的通项公式．
16．下列命题是真命题的是①④（填序号）．
①若A，B，C，D在一条直线上，则$\overrightarrow{AB}$与$\overrightarrow{CD}$是共线向量；
②若A，B，C，D不在一条直线上，则$\overrightarrow{AB}$与$\overrightarrow{CD}$不是共线向量；
③向量$\overrightarrow{AB}$与$\overrightarrow{CD}$是共线向量，则A，B，C，D四点必在一条直线上；
④向量$\overrightarrow{AB}$与$\overrightarrow{AC}$是共线向量，则A，B，C，D三点必在一条直线上．
3．空间四边形ABCD中，M、G分别是BC、CD的中点，则$\overrightarrow{MG}$-$\overrightarrow{AB}$+$\overrightarrow{AD}$等于（　　）
A．$\frac{3}{2}$$\overrightarrow{DB}$B．3$\overrightarrow{MG}$C．3$\overrightarrow{GM}$D．2$\overrightarrow{MG}$
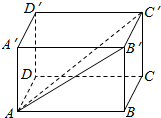13．如图，长方体ABCD-A′B′C′D′中，化简下列各式，并在图中标出化简得到的向量：
（1）$\overrightarrow{AA′}$-$\overrightarrow{CB}$；
（2）$\overrightarrow{AB′}$+$\overrightarrow{B′C′}$+$\overrightarrow{C′D′}$；
（3）$\frac{1}{2}$$\overrightarrow{AD}$+$\frac{1}{2}$$\overrightarrow{AB}$-$\frac{1}{2}$$\overrightarrow{A′A}$．
20．（1）函数y=lg（3-4x+x2）的定义域为A，当x∈A时，求f（x）=2x+2-3×4x的最值．
（2）已知函数f（x）=log0.5（x2-ax-a）的值域为R，且f（x）在（-∞，1-$\sqrt{3}$）上是增函数，求a的取值范围．
17．求下列圆的方程：
（1）已知点A（-4，-5），B（6，-1），以线段AB为直径的圆的方程．
（2）过两点C（-1，1）和D（1，3），圆心在x轴上的圆的标准方程．
2．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{1}{2}$，以坐标原点为圆心，椭圆的短半轴长为半径的圆与直线x-y+$\sqrt{6}$=0相切．
（1）求椭圆C的标准方程；
（2）设点P（4，0），A，B是椭圆C上关于x轴对称的任意两个不同的点，连结PB交椭圆C于另一点E，证明：直线AE与x轴相交于定点．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网