题目内容
13.如图,已知长方形ABCD中,AB=2$\sqrt{2}$,AD=$\sqrt{2}$,M为CD的中点,将△ADM沿AM折起,使得平面ADM⊥平面ABCM.(1)求证:AD⊥BM;
(2)在线段DB上是否存在点E,使得二面角E-AM-D的平面角为$\frac{π}{4}$?若存在,求出点E的位置;若不存在,请说明理由.

分析 (1)利用勾股定理逆定理证明AM⊥BM,从而得出BM⊥平面ADM,于是AD⊥BM;
(2)建立空间坐标系,设$\overrightarrow{DE}=λ\overrightarrow{DB}$,求出平面AME的法向量和平面ADM的法向量,令两法向量的夹角余弦值的绝对值为$\frac{\sqrt{2}}{2}$,解出λ即可判断λ的位置.
解答 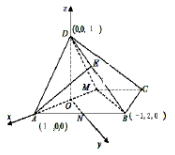 (1)证明:在矩形ABCD中,∵AD=$\sqrt{2}$,AB=2$\sqrt{2}$,M是CD的中点,
(1)证明:在矩形ABCD中,∵AD=$\sqrt{2}$,AB=2$\sqrt{2}$,M是CD的中点,
∴AM=BM=2,∴AM2+BM2=AB2,
∴AM⊥BM,又平面ADM⊥平面ABCM,平面ADM∩平面ABCM=AM,BM?平面ABCM,
∴BM⊥平面ADM,又AD?平面ADM,
∴AD⊥BM.
(2)解:取AM的中点O,AB的中点N,连结OD,ON,
则OD⊥平面ABCM,OA⊥ON,
以O为原点,以OA,ON,OD为轴建立空间坐标系,如图所示:
则A(1,0,0),B(-1,2,0),D(0,0,1),M(-1,0,0),
则$\overrightarrow{AM}$=(-2,0,0),$\overrightarrow{AD}$=(-1,0,1),$\overrightarrow{DB}$=(-1,2,-1),
设$\overrightarrow{DE}=λ\overrightarrow{DB}$=(-λ,2λ,-λ),则$\overrightarrow{AE}$=$\overrightarrow{AD}+\overrightarrow{DE}$=(-λ-1,2λ,1-λ),
设平面AME的一个法向量为$\overrightarrow{m}$=(x,y,z),则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{AM}=0}\\{\overrightarrow{m}•\overrightarrow{AE}=0}\end{array}\right.$,
∴$\left\{\begin{array}{l}{-2x=0}\\{(-λ-1)x+2λy+(1-λ)z=0}\end{array}\right.$,令y=1得$\overrightarrow{m}$=(0,1,$\frac{2λ}{λ-1}$),
又ON⊥平面ADM,∴$\overrightarrow{n}$=(0,1,0)是平面ADM的一个法向量,
∴cos<$\overrightarrow{m},\overrightarrow{n}$>=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$=$\frac{1}{1×\sqrt{1+\frac{4{λ}^{2}}{{λ}^{2}-2λ+1}}}$,
令$\frac{1}{1×\sqrt{1+\frac{4{λ}^{2}}{{λ}^{2}-2λ+1}}}$=$\frac{\sqrt{2}}{2}$,解得λ=$\frac{1}{3}$或λ=-1(舍).
∴当E为DB的靠近D的三等分点时,二面角E-AM-D的平面角为$\frac{π}{4}$.
点评 本题考查了线面垂直的判定与性质,空间向量与二面角的计算,属于中档题.

| A. | $-\frac{1}{2}$ | B. | 0 | C. | $\frac{1}{2}$ | D. | 2 |
| A. | 2 | B. | $\sqrt{2}$ | C. | $3-\sqrt{3}$ | D. | $3+\sqrt{3}$ |
| A. | -个圆 | B. | 一条射线 | C. | 半个圆 | D. | 一条直线 |
(1)如果按性别比例分层抽样,可以得到多少个不同的样本?(只要求写出算式,不必计算出结果);
(2)若这8人的数学成绩从小到大排序是65,68,72,79,81,88,92,95.物理成绩从小到大排序是72,77,80,84,86,90,93,98.
①求这8人中恰有3人数学、物理成绩均在85分以上的概率(结果用分数表示);
②已知随机抽取的8人的数学成绩和物理成绩如表:
| 学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 数学成绩 | 65 | 68 | 72 | 79 | 81 | 88 | 92 | 95 |
| 物理成绩 | 72 | 77 | 80 | 84 | 86 | 90 | 93 | 98 |
参考公式:相关系数:r=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sqrt{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}\sum_{i=1}^{n}({y}_{i}-\overline{y})^{2}}}$,R2=r2,
回归方程:$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$,其$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$
参考数据:$\overline{x}$=80,$\overline{y}$=85,$\sum_{i=1}^{8}$(xi-$\overline{x}$)2=868,$\sum_{i=1}^{8}$(yi-$\overline{y}$)2═518,$\sum_{i=1}^{8}$(xi-$\overline{x}$)(yi-$\overline{y}$)=664,$\sqrt{868}$≈29.5,$\sqrt{518}$≈22.8.