题目内容
18.求经过三点A(1,-1),B(1,4),C(4,2)的圆的方程,并求出圆的圆心与半径.分析 设出所求圆的一般式方程,把已知的三个点的坐标代入,得到关于D,E及F的三元一次方程组,求出方程组的解即可得到D,E及F的值,从而确定出圆的方程,把求出的圆的方程化为标准方程,即可找出圆心坐标和圆的半径.
解答 解:设所求圆的方程为x2+y2+Dx+Ey+F=0,
由已知,点A(1,-1),B(1,4),C(4,2)的坐标满足上述方程,
分别代入方程,可得$\left\{\begin{array}{l}{D-E+F+2=0}\\{D+4E+F+17=0}\\{4D+2E+F+20=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{D=-3}\\{E=-3}\\{F=-2}\end{array}\right.$,
所求圆的方程为:x2+y2-3x-3y-2=0,
化为标准方程为:(x-$\frac{3}{2}$)2+(y-$\frac{3}{2}$)2=$\frac{13}{2}$,
则圆的半径为r=$\frac{\sqrt{26}}{2}$,圆心坐标是($\frac{3}{2}$,$\frac{3}{2}$).
点评 此题考查了圆的一般方程,求圆方程的方法为待定系数法,此方法是先设出圆的一般方程,然后把已知的点代入到所设的方程中确定出圆方程中字母的值,从而确定出圆的方程.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
9.下列命题中错误的是( )
| A. | 两组对边分别相等的四边形是平行四边形 | |
| B. | 平行四边形的对边相等 | |
| C. | 对角线相等的四边形是矩形 | |
| D. | 矩形的对角线相等 |
8.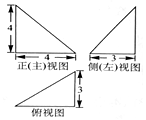 某四面体三视图如图所示,该四面体的体积为( )
某四面体三视图如图所示,该四面体的体积为( )
 某四面体三视图如图所示,该四面体的体积为( )
某四面体三视图如图所示,该四面体的体积为( )| A. | 8 | B. | 10 | C. | 20 | D. | 24 |
