题目内容
不等式sin（π+x）＞0成立的x的取值范围为（ ）
| A、（0，π） |
| B、（π，2π） |
| C、（2kπ，2kπ+π）（k∈Z） |
| D、（2kπ+π，2kπ+2π）（k∈Z） |
考点：正弦函数的定义域和值域
专题：三角函数的图像与性质
分析：令2kπ+2π＜π+x＜2kπ+3π，解不等式可得．
解答：
解：令2kπ+2π＜π+x＜2kπ+3π，
解得2kπ+π＜x＜2kπ+2π，
∴所求x的取值范围为（2kπ+π，2kπ+2π）（k∈Z）
故选：D．
解得2kπ+π＜x＜2kπ+2π，
∴所求x的取值范围为（2kπ+π，2kπ+2π）（k∈Z）
故选：D．
点评：本题考查正弦函数的值域，属基础题．
练习册系列答案
相关题目
如图，AB是的直径，PB，PE分别切⊙O于B，C，∠ACE=40°，则∠P=（ ）
| A、60° | B、70° |
| C、80° | D、90° |
已知l是直线，α、β是两个不同平面，下列命题中的真命题是（ ）
| A、若l∥α，l∥β，则α∥β |
| B、若α⊥β，l∥α，则l⊥β |
| C、若l⊥α，l∥β，则α⊥β |
| D、若l∥α，α∥β，则l∥β |
若{an}为等差数列，Sn是其前n项和，且S11=
，则tana6=（ ）
| 88π |
| 3 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
正方形ABCD的边长为3，点E在边AB上，点F在边BC上，AE=BF=1，动点P从点E出发沿直线向F运动，每当碰到正方形的边时反弹，反弹时反射角等于入射角．当点P第一次碰到点E时，P与正方形的边碰撞的次数为（ ）
| A、8 | B、6 | C、4 | D、3 |
一个几何体的三视图及尺寸如图所示，则该几何体的体积为（ ）
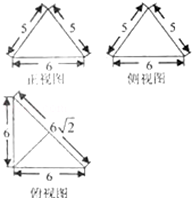
| A、48 | B、72 | C、12 | D、24 |
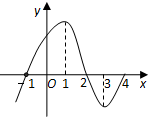如图所示为y=f′（x）的图象，则下列判断正确的是（ ）